指数分布是连续概率分布的一种,常用于描述等待时间、寿命等随机变量的分布。
1. 标准形式的指数分布
标准形式的指数分布的概率密度函数(PDF)为:
f
(
x
;
λ
)
=
{
λ
e
−
λ
x
if
x
≥
0
0
if
x
f(x;λ)={λe−λx0if x≥0if x0
其中,
λ
>
0
lambda > 0
λ>0 是速率参数(rate parameter),表示单位时间内发生某事件的平均次数。
- 累积分布函数(CDF):
F
(
x
;
λ
)
=
{
1
−
e
−
λ
x
if
x
≥
0
0
if
x
F(x;λ)={1−e−λx0if x≥0if x0
- 期望(均值):
1
λ
frac{1}{lambda}
λ1 - 方差:
1
λ
2
frac{1}{lambda^2}
λ21
2. 通过尺度参数变换的指数分布
为了和正态分布PDF等其他指数家族函数作类比分析,也会使用尺度参数(scale parameter)
θ
theta
θ 来代替率参数
λ
lambda
λ。此时,概率密度函数变为:
f
(
x
;
θ
)
=
{
1
θ
e
−
x
θ
if
x
≥
0
0
if
x
f(x;θ)={θ1e−θx0if x≥0if x0
其中,
θ
>
0
theta > 0
θ>0 是尺度参数,表示平均等待时间或平均寿命等。
-
注意:这里的
θ
theta
θ 和
λ
lambda
λ 是倒数关系,即
θ
=
1
λ
theta = frac{1}{lambda}
θ=λ1。
-
累积分布函数(CDF):
F
(
x
;
θ
)
=
{
1
−
e
−
x
θ
if
x
≥
0
0
if
x
F(x;θ)={1−e−θx0if x≥0if x0
- 期望(均值):
θ
theta
θ - 方差:
θ
2
theta^2
θ2
在这种表示下,
θ
theta
θ是分布的均值,它的极大似然估计是样本均值。
λ
lambda
λ 越小,也就是
θ
theta
θ越大越拖尾。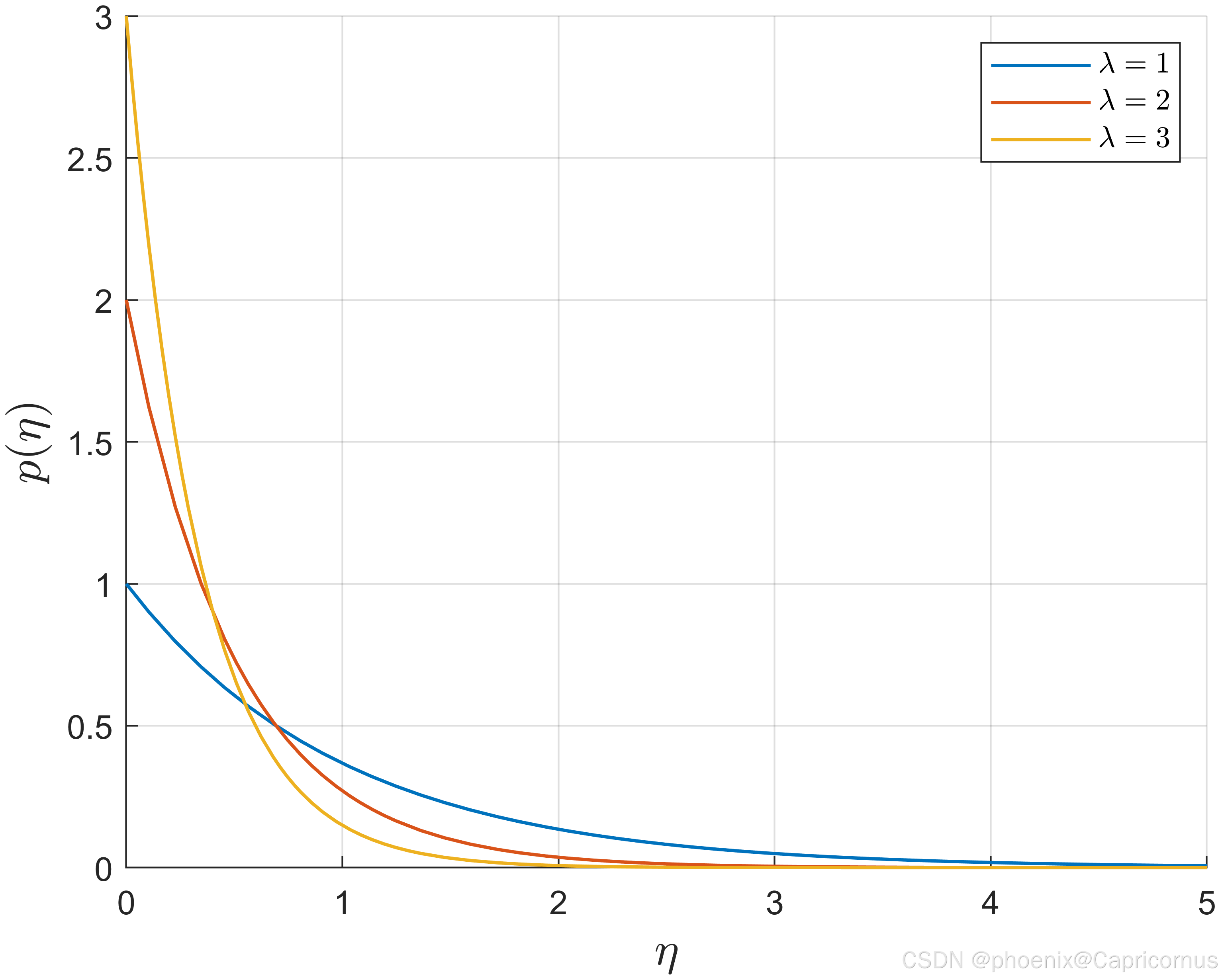
MATLAB中,expfit和mle函数计算参数的极大似然估计。
很神奇,很多分布的PDF都是指数函数。例如常见的高斯函数,也就是正态分布的概率密度函数也是指数家族函数:
f
(
x
∣
μ
,
σ
2
)
=
1
2
π
σ
2
e
−
(
x
−
μ
)
2
2
σ
2
f(x|mu,sigma^2) = frac{1}{sqrt{2pisigma^2}} e^{-frac{(x-mu)^2}{2sigma^2}}
f(x∣μ,σ2)=2πσ21e−2σ2(x−μ)2
方差
σ
2
sigma^2
σ2 越小,曲线越陡峭,表示数据越集中;方差越大,曲线越平坦,表示数据越分散。

评论(0)