【机器学习】从零开始理解深度学习——揭开神经网络的神秘面纱-清扬资源网

1. 引言

随着技术的飞速发展，人工智能（AI）已从学术研究的实验室走向现实应用的舞台，成为推动现代社会变革的核心动力之一。而在这一进程中，深度学习（Deep Learning）因其在大规模数据处理和复杂问题求解中的卓越表现，迅速崛起为人工智能的最前沿技术。深度学习的核心是神经网络，它模仿了生物神经系统的工作原理，通过层层叠加的结构化模型，逐步从数据中学习到有用的特征，从而完成分类、识别、生成等任务。

现代人工智能的飞跃不仅依赖于算法的进步，还得益于数据规模的爆炸式增长和计算资源的快速提升。深度学习正是在大数据、GPU计算等因素的推动下，才得以突破过去的技术瓶颈，进入大规模应用阶段。这一转变带来了跨行业的变革，涵盖了从图像识别、自然语言处理到自动驾驶、医疗诊断等诸多领域。

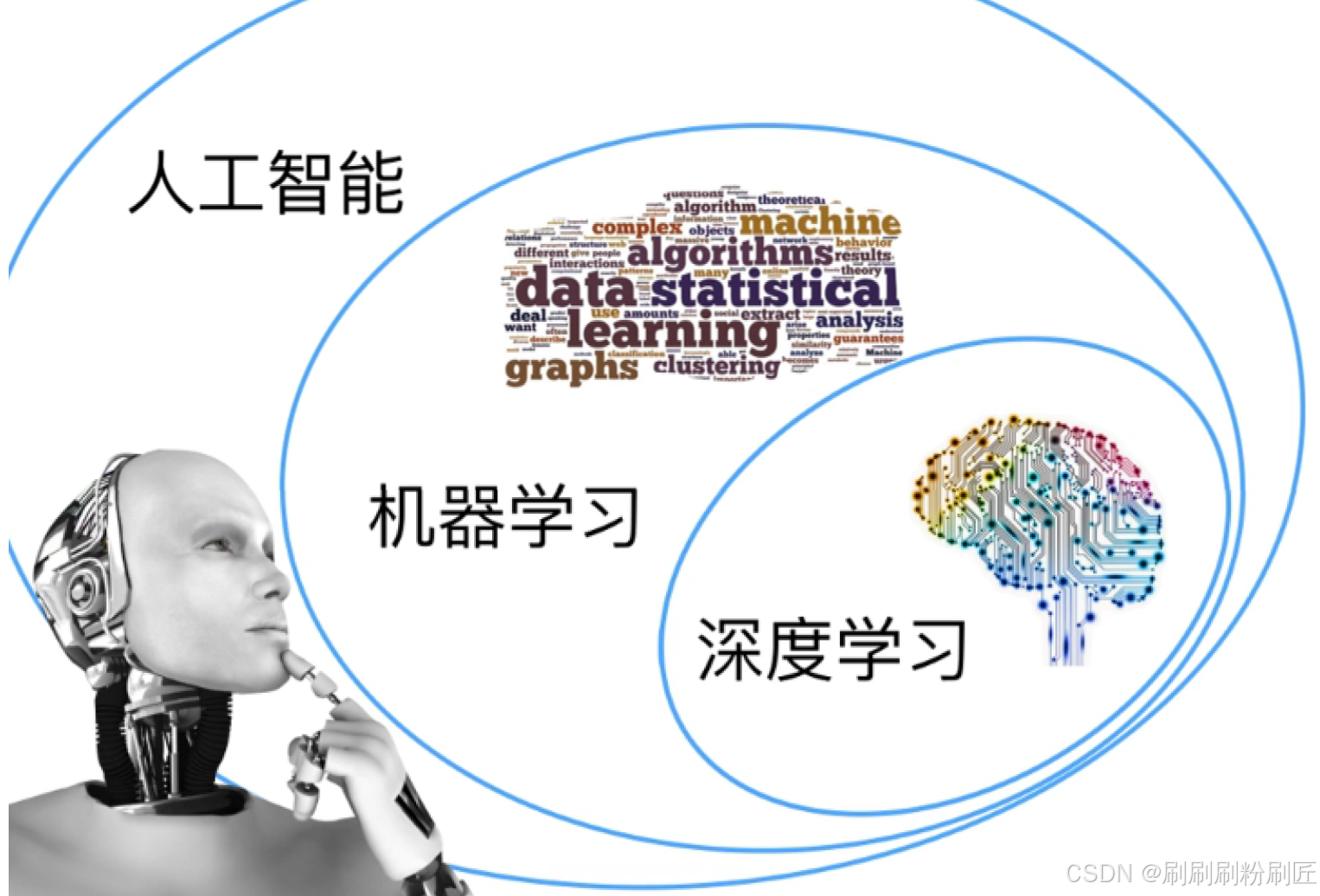
1.1深度学习的背景与重要性

深度学习是机器学习的一个分支，机器学习又属于更广泛的人工智能范畴。在传统的机器学习模型中，最关键的部分是特征工程，模型的性能高度依赖于手工设计的特征。专家必须针对不同的任务和领域对数据进行复杂的特征提取和转换，以使模型能够更好地识别其中的模式。这种方式不仅费时费力，而且对高维度、非结构化的数据（如图像、音频、文本）往往无能为力。

与传统机器学习模型不同，深度学习采用了“端到端学习”的方式，能够自动从数据中学习特征表示，省去了繁琐的特征工程环节。这种自动化特征提取的能力，尤其在处理大规模非结构化数据（如图像、视频、语音和文本）时表现出色，从而极大拓展了人工智能的应用场景。例如，深度学习算法如今广泛应用于自动驾驶车辆中的物体检测、人脸识别系统、智能语音助手以及机器翻译等实际任务。

1.2神经网络的回归与突破

深度学习的成功主要依赖于神经网络的重新兴起。神经网络的概念最早可以追溯到20世纪50年代，然而由于早期的计算能力限制以及反向传播算法等关键技术尚未成熟，神经网络一度被认为难以实用化。然而，随着反向传播算法的引入，以及20世纪90年代后计算能力的飞速发展，神经网络得以重新进入研究者的视野，并逐渐发展成为现代深度学习的核心技术。

神经网络通过仿生学的思维模拟生物神经元之间的连接，构建了一种多层次的、可学习的架构。这种架构不仅能够捕捉数据中的简单模式，还可以通过增加隐藏层（即加深网络深度）学习到更为抽象和复杂的特征。神经网络的这种层次化学习能力，是传统机器学习算法难以企及的。

1.3深度学习的现实应用与挑战

深度学习的迅速崛起带来了大量创新性的应用。以图像处理为例，卷积神经网络（CNN）通过其独特的卷积层结构，能够有效识别图片中的物体和模式，广泛应用于人脸识别、医疗影像诊断等领域。在自然语言处理（NLP）领域，深度学习模型如RNN和Transformer则极大地提升了文本理解与生成的能力，使得机器翻译、情感分析和语音识别等应用变得更加精准。

然而，深度学习也面临一些严峻的挑战。首先，深度神经网络依赖于大量的标注数据和庞大的计算资源，导致其应用成本较高。其次，尽管深度学习在各种任务中展现了卓越的表现，但其**“黑箱”特性让人们难以理解模型的内部工作原理，这在安全性和可解释性要求较高的应用（如医疗或金融）中引发了担忧。最后，如何应对数据隐私和公平性**的问题，也是深度学习走向大规模应用过程中必须解决的重要议题。

1.4本文的结构

为了帮助读者系统性地理解深度学习及其核心组件——神经网络，本文将从以下几个方面逐步深入：

首先介绍神经网络的基本概念，并逐步展开到复杂的网络结构。
解释神经网络的前馈、反向传播以及梯度下降等基本算法。
详细探讨深度神经网络的工作原理，以及其在多个领域的实际应用。
最后，本文将展望深度学习未来的发展趋势与挑战，并提出在实际工业和学术研究中的一些借鉴与建议。

通过本文的阐述，读者不仅可以掌握从零开始理解深度学习的基本原理，还能在行业应用中找到相应的指导和启示。

2. 什么是神经网络？

神经网络（Neural Network） 是一种模仿人类大脑神经系统的计算模型，由大量互联的人工神经元（也称为节点或单元）构成。其核心思想是模拟生物神经系统的层次化结构，以层与层之间的连接权重传递信息，并通过不断的调整权重，使得网络能够从数据中学习到有效的特征和规律。神经网络已经成为深度学习中的基础架构，广泛应用于多个领域，包括图像识别、语音识别、自然语言处理等。

2.1 神经网络的基本结构

神经网络的结构通常可以划分为以下几个部分：

输入层（Input Layer）：负责接收外部输入数据。每个输入节点对应于输入数据的一个特征。
隐藏层（Hidden Layer）：介于输入层和输出层之间的层。隐藏层中的节点通过连接权重接收输入层的数据，并将信息进行复杂的处理。这一层是神经网络学习特征的核心。
输出层（Output Layer）：负责输出预测结果。输出层中的节点数取决于具体的任务，例如分类问题中的类别数量或回归问题中的输出维度。

简单的神经网络称为前馈神经网络（Feedforward Neural Network, FNN），即信息从输入层经隐藏层传递到输出层，中间没有反馈循环。对于更复杂的任务，网络可以通过增加多个隐藏层来构建深度神经网络（Deep Neural Network, DNN），以处理更为复杂的特征表示。

神经网络的基本结构示意图：

Input Layer   ->   Hidden Layer(s)   ->   Output Layer
 [x1, x2, x3] -> [h1, h2, h3, h4] -> [y1, y2]

在实际应用中，神经网络通过反复更新连接权重来学习数据中的模式。这种学习过程是通过一系列优化算法（如梯度下降）来实现的。

2.2 神经元的数学模型

每个神经元可以视为一个函数，接受输入并输出一个值。其核心工作流程如下：

加权求和：神经元接收来自上一层的输入，每个输入都与一个权重相乘，并进行求和。设输入为 $x_{1},x_{2},...,x_{n}$ ，对应的权重为 $w_{1},w_{2},...,w_{n}$ ，则加权和为：

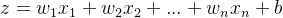
$z = w_{1}x_{1} + w_{2}x_{2} + ...+ w_{n}x_{n} + b$

其中， b是偏置项（bias），用于调整模型的输出，使其不完全依赖输入的线性组合。
激活函数：为了引入非线性特性，神经元会将加权和 zzz 通过一个激活函数（Activation Function）处理。常见的激活函数包括Sigmoid、ReLU和Tanh等。激活函数输出的结果决定了神经元的输出信号强度。
输出：神经元的输出值将作为下一层神经元的输入。

神经元的数学模型示意图：

    Input: x1, x2, ..., xn
        |
     Weights: w1, w2, ..., wn
        |
    Summation: z = Σ(wi * xi) + b
        |
  Activation Function: f(z)
        |
      Output

代码示例：实现一个简单的神经元

import numpy as np

# 定义激活函数（Sigmoid）
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

# 实现单个神经元的前向传播
def neuron_forward(x, w, b):
    """
    x: 输入 (numpy array)
    w: 权重 (numpy array)
    b: 偏置 (scalar)
    """
    # 加权求和
    z = np.dot(w, x) + b
    # 激活函数
    output = sigmoid(z)
    return output

# 示例数据
x = np.array([0.5, -0.2, 0.1])  # 输入
w = np.array([0.4, 0.3, 0.7])   # 权重
b = -0.5  # 偏置

# 前向传播
output = neuron_forward(x, w, b)
print(f"Neuron Output: {output}")

在上面的示例中，我们定义了一个简单的神经元，该神经元接收输入 xxx ，通过加权求和和激活函数（Sigmoid）处理后，输出结果。

2.3 神经网络的学习机制

神经网络的强大之处在于它能够通过数据自动调整权重和偏置，以最小化预测结果与真实值之间的误差。这一过程通常称为学习或训练。具体来说，神经网络的学习过程包含以下几个步骤：

前向传播（Forward Propagation）：输入数据通过网络的每一层进行计算，最终生成输出。
计算误差（Error Calculation）：通过损失函数（如均方误差或交叉熵损失）计算网络预测值与真实标签之间的误差。
反向传播（Backpropagation）：通过反向传播算法，误差从输出层逐层传回网络，并更新每个神经元的权重和偏置。反向传播基于梯度下降原理，沿着损失函数的梯度方向调整权重，以减小误差。
权重更新：根据学习率和梯度的大小，更新每个神经元的权重和偏置。

代码示例：使用简单的梯度下降更新神经元的权重

# 定义损失函数（均方误差）
def mse_loss(y_true, y_pred):
    return np.mean((y_true - y_pred) ** 2)

# 简单的梯度下降算法更新权重
def gradient_descent(x, y_true, w, b, learning_rate):
    """
    x: 输入
    y_true: 真实标签
    w: 权重
    b: 偏置
    learning_rate: 学习率
    """
    # 前向传播
    y_pred = neuron_forward(x, w, b)
    
    # 计算损失
    loss = mse_loss(y_true, y_pred)
    
    # 计算梯度（假设简单的均方误差损失函数的导数）
    dw = -2 * (y_true - y_pred) * x
    db = -2 * (y_true - y_pred)
    
    # 更新权重和偏置
    w -= learning_rate * dw
    b -= learning_rate * db
    
    return w, b, loss

# 示例训练过程
y_true = 0.8  # 真实标签
learning_rate = 0.01

for epoch in range(100):
    w, b, loss = gradient_descent(x, y_true, w, b, learning_rate)
    if epoch % 10 == 0:
        print(f"Epoch {epoch}, Loss: {loss:.4f}")

2.4 神经网络的优势与应用

神经网络的最大优势在于其强大的非线性特征学习能力，它能够自动从复杂、庞大的数据中提取有用的模式，而不依赖于人工设计的特征。这使得神经网络在许多高维度数据（如图像、语音、文本）的处理任务中表现优越。

典型的应用领域包括：

图像分类和检测：利用卷积神经网络（CNN）识别图片中的对象。
自然语言处理：通过循环神经网络（RNN）和Transformer模型实现文本生成、情感分析、机器翻译等任务。
语音识别：神经网络能将语音信号转换为文本或语义信息。

总结而言，神经网络为解决复杂的、非线性问题提供了一个高效的工具，尤其在大规模数据驱动的任务中，展现了无与伦比的性能和潜力。

3. 前馈神经网络 (Feedforward Neural Network, FNN)

前馈神经网络（Feedforward Neural Network, FNN） 是最基础的人工神经网络之一，其特点是信息从输入层开始，依次通过隐藏层向前传递，直到到达输出层。与一些其他类型的神经网络（如循环神经网络，RNN）不同，FNN 中的数据流是单向的，网络中没有环路，即信息不会回传至前面的层。FNN 是深度学习中许多复杂模型的基础，它构建了神经网络的简单结构，并为更复杂的网络提供了基础。

3.1 FNN 的基本架构

前馈神经网络由多个节点组成，这些节点分布在多个层次，包括：

输入层：直接接收输入数据，每个节点代表一个输入特征。在实际应用中，输入可以是多维的，如一个图像的像素、音频信号、或文本的词向量。
隐藏层：这是网络的核心部分，由一个或多个隐藏层组成。每个节点都通过权重连接与前一层的所有节点相连，并通过激活函数计算输出值。这些层的数量和每层的节点数可以根据任务复杂度进行调整。
输出层：将隐藏层的输出转换为最终的预测结果。输出层的节点数量通常根据具体任务决定。例如，二分类任务通常只有一个输出节点，而多分类任务则会有多个输出节点。

前馈神经网络的基本结构示意图：

输入层 -> 隐藏层1 -> 隐藏层2 -> ... -> 输出层

3.2 FNN 的工作原理

前馈神经网络的核心工作流程可以分为两个阶段：前向传播和反向传播。

前向传播（Forward Propagation）
在前向传播中，输入数据逐层向前传递，从输入层开始，经过隐藏层，最后到达输出层。在每一层，每个神经元都会接收来自前一层的输入，进行加权求和，并通过激活函数生成输出。这一过程本质上是一个非线性映射，将输入数据转换为输出结果。
反向传播（Backpropagation）
反向传播是前馈神经网络的学习过程，它通过计算预测值与真实标签之间的误差，利用梯度下降法调整每个神经元的权重和偏置，使得误差逐步减少。反向传播本质上是一个链式求导的过程，将误差从输出层逐层传播回输入层，并更新每层的权重。

3.3 数学模型

前馈神经网络的核心计算可以通过以下数学公式来描述：

前向传播：
对于每个隐藏层的神经元 $h_{j}$ ，它接收来自上一层所有节点的输入，并通过权重 $w_{ij}$ 和偏置 $b_{j}$ 进行加权求和：

$z_{j} = sum_{i = 1}^{n}w_{ij}x_{i} + b_{j}$

其中， $x_{i}$ 是输入， $w_{ij}$ 是权重， $b_{j}$ 是偏置项， $z_{j}$ 是加权求和的结果。

接下来，使用激活函数（如 ReLU 或 Sigmoid）对 $z_{j}$ 进行非线性变换：

$h_{j} = fleft ( z_{j} right )$

其中，fff 是激活函数，如。
输出层：
最后，在输出层中，前一层的输出会被转换为最终的预测值 yyy。对于分类问题，输出层的激活函数通常是Softmax，它将输出转换为概率分布：

$y_{k} = frac{e^{z_{k}}}{sum_{j = 1}^{K}e^{z_{j}}}$

其中 $y_{k}$ 是类别 k 的预测概率。

3.4 前馈神经网络的训练

前馈神经网络的训练过程包括以下几个步骤：

初始化参数：随机初始化网络的权重和偏置。
前向传播：将输入数据逐层传递到输出层，计算每个节点的输出值。
计算损失：通过损失函数计算网络的预测输出与真实标签之间的误差。常见的损失函数包括均方误差（用于回归任务）和交叉熵损失（用于分类任务）。
反向传播：通过反向传播算法，计算每个参数对误差的梯度，并根据梯度下降法更新权重和偏置，使得损失函数的值逐步减小。
参数更新：根据学习率和梯度调整参数，重复上述过程，直至模型收敛。

代码示例：实现一个简单的前馈神经网络

以下代码展示了如何使用 Python 和 numpy 实现一个简单的前馈神经网络，并通过随机梯度下降（SGD）训练模型。

import numpy as np

# 定义激活函数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def sigmoid_derivative(x):
    return x * (1 - x)

# 前馈神经网络类
class FeedforwardNeuralNetwork:
    def __init__(self, input_size, hidden_size, output_size):
        # 初始化权重和偏置
        self.w1 = np.random.rand(input_size, hidden_size)  # 输入层到隐藏层的权重
        self.b1 = np.random.rand(1, hidden_size)           # 隐藏层的偏置
        self.w2 = np.random.rand(hidden_size, output_size) # 隐藏层到输出层的权重
        self.b2 = np.random.rand(1, output_size)           # 输出层的偏置

    def forward(self, X):
        # 前向传播
        self.z1 = np.dot(X, self.w1) + self.b1  # 隐藏层输入
        self.a1 = sigmoid(self.z1)              # 隐藏层输出
        self.z2 = np.dot(self.a1, self.w2) + self.b2  # 输出层输入
        self.a2 = sigmoid(self.z2)                   # 输出层输出
        return self.a2

    def backward(self, X, y, output, learning_rate):
        # 计算输出层误差
        error = y - output
        d_output = error * sigmoid_derivative(output)

        # 计算隐藏层误差
        hidden_error = d_output.dot(self.w2.T)
        d_hidden = hidden_error * sigmoid_derivative(self.a1)

        # 更新权重和偏置
        self.w2 += self.a1.T.dot(d_output) * learning_rate
        self.b2 += np.sum(d_output, axis=0, keepdims=True) * learning_rate
        self.w1 += X.T.dot(d_hidden) * learning_rate
        self.b1 += np.sum(d_hidden, axis=0, keepdims=True) * learning_rate

    def train(self, X, y, epochs, learning_rate):
        for epoch in range(epochs):
            # 前向传播
            output = self.forward(X)
            # 反向传播
            self.backward(X, y, output, learning_rate)
            if epoch % 100 == 0:
                loss = np.mean(np.square(y - output))  # 均方误差
                print(f"Epoch {epoch}, Loss: {loss}")

# 示例：训练前馈神经网络
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])  # 输入数据
y = np.array([[0], [1], [1], [0]])  # XOR 输出

# 初始化网络
nn = FeedforwardNeuralNetwork(input_size=2, hidden_size=2, output_size=1)
# 训练网络
nn.train(X, y, epochs=1000, learning_rate=0.1)

# 测试
output = nn.forward(X)
print("Predicted Output: n", output)

在此代码中，我们实现了一个包含两层（隐藏层和输出层）的前馈神经网络，并使用随机梯度下降算法更新网络的权重和偏置。该网络用于解决 XOR 问题，这是一个经典的非线性分类问题。

3.5 FNN 的实际应用

前馈神经网络尽管简单，但在许多应用中都有较好的表现，尤其是在需要进行非线性决策的任务中。具体应用包括：

图像分类：前馈神经网络作为卷积神经网络（CNN）的基础结构，被广泛应用于图像分类任务。
回归分析：在连续数值预测（如房价预测）中，FNN 也被用作基本模型。
时间序列预测：虽然 FNN 并不适合处理时间依赖的数据，但其经过适当调整后，仍可以用于某些时间序列预测任务。

3.6 研究方向与挑战

前馈神经网络的局限性在于其结构较为简单，且随着网络深度的增加，训练过程容易出现梯度消失或梯度爆炸问题。因此，在深度学习领域，研究人员不断探索改进算法和优化策略，如引入更多复杂的激活函数、优化算法以及深度网络结构（如 ResNet、VGG 等），以提升网络的表现能力。

总结而言，前馈神经网络虽然是最基础的神经网络架构，但它为深度学习的理论和实践奠定了重要的基础，许多复杂的网络结构都是基于 FNN 扩展而来的。

4. 反向传播与梯度下降

反向传播（Backpropagation） 和 梯度下降（Gradient Descent） 是深度学习中最重要的核心技术之一。它们共同构成了神经网络的学习机制，用来调整网络中的参数（如权重和偏置），以最小化模型的预测误差。

4.1 反向传播的基本原理

反向传播是神经网络的训练算法，旨在通过误差的逐层回传来计算每个参数对误差的贡献，并据此更新参数。反向传播的核心思想是基于 链式法则（Chain Rule） 的梯度计算，通过计算损失函数相对于网络各层参数的偏导数，确定这些参数如何影响误差大小。

反向传播的过程通常与 前向传播（Forward Propagation） 配合使用：

前向传播：输入数据从输入层逐层传递至输出层，计算每个神经元的输出，最终得到预测结果。
误差计算：通过损失函数计算网络输出与真实标签之间的差异，损失函数可以是均方误差（MSE）或交叉熵损失（Cross-Entropy Loss）。
反向传播：从输出层开始，逐层计算误差对每个参数的梯度，并利用这些梯度更新参数。反向传播的目标是通过优化算法（如梯度下降）使网络的总误差最小化。

4.2 梯度下降的原理

梯度下降是一种优化算法，作用是在损失函数的梯度方向上更新模型的参数，使损失函数的值逐渐减少。其基本思路是，通过迭代地调整参数，沿着损失函数下降最快的方向进行步进，直到找到一个局部最小值或全局最小值。

梯度下降的更新公式如下：

$theta := theta - alpha frac{partial Jleft ( theta right )}{partial theta }$

其中：

表示待优化的参数（如权重和偏置）；
表示损失函数；
$frac{partial Jleft ( theta right )}{partial theta }$ 表示损失函数对参数的梯度；
是学习率，决定了每次更新的步长。

梯度下降的类型

梯度下降算法有不同的变种，常见的包括：

批量梯度下降（Batch Gradient Descent）：使用整个训练集计算梯度，更新参数。这种方法在每次迭代中都能获得精确的梯度，但计算代价较高。
随机梯度下降（Stochastic Gradient Descent, SGD）：在每次迭代中只使用一个样本来计算梯度并更新参数，这使得更新更加频繁，但梯度较为噪声化，可能导致更新方向不稳定。
小批量梯度下降（Mini-Batch Gradient Descent）：每次迭代使用一个小批量数据计算梯度，结合了批量梯度下降和随机梯度下降的优点，既提高了计算效率，又能保证较为平滑的梯度更新。

4.3 反向传播与梯度下降的结合

反向传播与梯度下降密不可分，反向传播为梯度下降算法提供了每个参数的梯度信息，而梯度下降则通过这些梯度调整网络参数。具体流程如下：

前向传播：输入通过网络进行前向传播，计算每层的激活值和最终输出。
误差计算：根据损失函数计算输出层的误差。
反向传播：从输出层开始，将误差反向传递到隐藏层，逐层计算每个参数对损失函数的导数（梯度）。
梯度更新：使用梯度下降或其变种更新每个参数，减小损失函数的值。
重复：上述过程会持续进行，直到损失函数收敛到一个最小值。

4.4 反向传播算法的数学推导

以一个单层的神经网络为例，假设输出层的损失函数为交叉熵损失，激活函数为 Sigmoid，我们可以推导出其梯度计算过程：

损失函数：假设输出为 y，预测值为，损失函数为交叉熵损失：

其中，是 Sigmoid 函数的输出：

$hat{y} = sigma left ( z right )=frac{1}{1+e^{-z}}$
反向传播计算梯度：对于输出层的权重 w，损失函数对权重的导数可以通过链式法则计算：

$frac{partial L}{partial w} = frac{partial L}{partial hat{y}} cdot frac{partial hat{y}}{partial z} cdot frac{partial z}{partial w}$

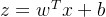其中 $z=w^{T}x + b$ ，是输入的加权和，梯度链依次通过各层传递。

4.5 代码示例：实现反向传播与梯度下降

以下代码展示了如何通过简单的 Python 和 numpy 实现反向传播算法，并使用随机梯度下降进行权重更新。

import numpy as np

# 定义 Sigmoid 激活函数及其导数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def sigmoid_derivative(x):
    return x * (1 - x)

# 神经网络类
class SimpleNeuralNetwork:
    def __init__(self, input_size, hidden_size, output_size):
        # 初始化权重和偏置
        self.w1 = np.random.randn(input_size, hidden_size)
        self.b1 = np.zeros((1, hidden_size))
        self.w2 = np.random.randn(hidden_size, output_size)
        self.b2 = np.zeros((1, output_size))

    # 前向传播
    def forward(self, X):
        self.z1 = np.dot(X, self.w1) + self.b1
        self.a1 = sigmoid(self.z1)
        self.z2 = np.dot(self.a1, self.w2) + self.b2
        self.a2 = sigmoid(self.z2)
        return self.a2

    # 反向传播
    def backward(self, X, y, output, learning_rate):
        # 输出层误差
        output_error = y - output
        output_delta = output_error * sigmoid_derivative(output)

        # 隐藏层误差
        hidden_error = output_delta.dot(self.w2.T)
        hidden_delta = hidden_error * sigmoid_derivative(self.a1)

        # 更新权重和偏置
        self.w2 += self.a1.T.dot(output_delta) * learning_rate
        self.b2 += np.sum(output_delta, axis=0, keepdims=True) * learning_rate
        self.w1 += X.T.dot(hidden_delta) * learning_rate
        self.b1 += np.sum(hidden_delta, axis=0, keepdims=True) * learning_rate

    # 训练模型
    def train(self, X, y, epochs, learning_rate):
        for epoch in range(epochs):
            output = self.forward(X)
            self.backward(X, y, output, learning_rate)
            if epoch % 100 == 0:
                loss = np.mean(np.square(y - output))
                print(f'Epoch {epoch}, Loss: {loss}')

# 示例：训练网络
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])  # 输入数据
y = np.array([[0], [1], [1], [0]])  # XOR 输出

# 初始化网络
nn = SimpleNeuralNetwork(input_size=2, hidden_size=2, output_size=1)

# 训练网络
nn.train(X, y, epochs=1000, learning_rate=0.1)

# 测试
output = nn.forward(X)
print("Predicted Output: n", output)

在这段代码中，我们创建了一个简单的神经网络并实现了反向传播算法。该网络用于解决 XOR 问题，并通过随机梯度下降优化其权重。每次迭代中，网络通过反向传播计算梯度，随后利用梯度下降更新权重和偏置，以减小预测误差。

4.6 反向传播与梯度下降的局限性

尽管反向传播和梯度下降是神经网络训练中的核心技术，但它们也存在一定的局限性和挑战：

梯度消失和梯度爆炸：在深度神经网络中，随着梯度在层间传递，其值可能会逐渐变小（梯度消失）或变大（梯度爆炸），这会导致训练不稳定或难以收敛。
学习率选择：学习率过大可能导致训练过程振荡不收敛，学习率过小则会导致训练过程缓慢。
局部最小值问题：梯度下降有时会陷入局部最小值，而非全局最优解。对此，研究人员提出了多种改进算法，如动量梯度下降、RMSprop、Adam 等，以提高优化过程的稳定性和效率。

反向传播和梯度下降虽然是深度学习中必不可少的技术，但研究人员仍在不断优化这些方法，以应对深度学习模型的复杂性和多样性。

5. 深度神经网络 (Deep Neural Network, DNN)

深度神经网络（Deep Neural Network, DNN）是人工神经网络的一种扩展，其特点是拥有多个隐藏层。DNN 是深度学习的核心模型，广泛应用于图像识别、自然语言处理、语音识别等复杂任务。随着层数的增加，DNN 可以学习更抽象的特征表示，从而在各类任务中取得显著的效果。

5.1 DNN 的结构

与传统的浅层神经网络（仅有一两个隐藏层）不同，DNN 包含多个隐藏层，每层由多个神经元组成，彼此通过权重相连接。每个神经元接收来自上一层的输入，并通过激活函数（如 ReLU 或 Sigmoid）将其非线性变换为输出，输入下一层。

DNN 的基本组成包括：

输入层（Input Layer）：接收原始数据输入，如图像的像素值或文本的词向量。
隐藏层（Hidden Layers）：通过权重和激活函数逐层转换数据特征，提取逐步抽象的特征表示。
输出层（Output Layer）：生成最终的输出，如分类问题中的类别概率，或回归问题中的数值预测。

5.2 深度神经网络的工作原理

DNN 的工作流程包括前向传播（Forward Propagation） 和 反向传播（Backpropagation） 两个阶段。

前向传播：数据从输入层开始，通过各个隐藏层的神经元逐层计算输出值。每个神经元将输入与权重相乘后加上偏置，再通过激活函数生成输出，输入下一层。这一过程在网络中的所有神经元上并行进行，最终得出输出层的结果。
反向传播：通过与真实标签比较，使用损失函数计算预测结果的误差，接着通过反向传播算法计算各层参数的梯度，使用梯度下降等优化算法调整网络权重，从而最小化损失函数。

5.3 DNN 的优点

相比于浅层神经网络，DNN 拥有更强的表达能力和泛化能力，能够更有效地处理复杂问题。这些优点主要体现在以下几个方面：

自动特征提取：DNN 的多层结构允许模型通过层层转换自动提取特征，无需人工设计特征工程，这在处理图像、文本等高维数据时尤为显著。
深层次特征表示：多层网络可以逐层抽象数据中的复杂特征，前几层提取简单的低级特征（如边缘、颜色），而后几层则可以学到更加抽象的高级特征（如物体的轮廓、语义信息）。
更强的拟合能力：相比于浅层模型，DNN 可以处理更复杂的非线性关系，在大规模数据集上通常具有更好的表现。

5.4 深度神经网络的训练

深度神经网络的训练与浅层网络类似，但由于层数增加，训练过程中的计算复杂度和数据需求也相应增加。训练 DNN 的关键步骤如下：

初始化参数：通常使用随机初始化或 He/Xavier 初始化方法来设定权重。初始化不当可能会导致梯度消失或梯度爆炸。
前向传播：将输入数据逐层传递至输出层，计算每层神经元的激活值。
损失函数：通过损失函数（如均方误差、交叉熵损失）计算输出与目标值之间的差异。
反向传播：根据误差逐层计算梯度，并将梯度沿着反向路径传递到前几层，以更新权重和偏置。
优化算法：使用梯度下降或其变种（如 Adam、RMSprop 等）更新网络的参数，最小化损失函数。

5.5 代码示例：构建简单的深度神经网络

以下是一个简单的 Python 代码示例，使用 numpy 构建一个两层的深度神经网络，用于二分类任务。

import numpy as np

# 定义激活函数及其导数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def sigmoid_derivative(x):
    return x * (1 - x)

# 构建深度神经网络
class DeepNeuralNetwork:
    def __init__(self, input_size, hidden_size, output_size):
        # 初始化权重和偏置
        self.w1 = np.random.randn(input_size, hidden_size) * 0.1
        self.b1 = np.zeros((1, hidden_size))
        self.w2 = np.random.randn(hidden_size, hidden_size) * 0.1
        self.b2 = np.zeros((1, hidden_size))
        self.w3 = np.random.randn(hidden_size, output_size) * 0.1
        self.b3 = np.zeros((1, output_size))
    
    # 前向传播
    def forward(self, X):
        self.z1 = np.dot(X, self.w1) + self.b1
        self.a1 = sigmoid(self.z1)
        self.z2 = np.dot(self.a1, self.w2) + self.b2
        self.a2 = sigmoid(self.z2)
        self.z3 = np.dot(self.a2, self.w3) + self.b3
        self.a3 = sigmoid(self.z3)
        return self.a3

    # 反向传播
    def backward(self, X, y, output, learning_rate):
        output_error = y - output
        output_delta = output_error * sigmoid_derivative(output)

        hidden_error2 = output_delta.dot(self.w3.T)
        hidden_delta2 = hidden_error2 * sigmoid_derivative(self.a2)

        hidden_error1 = hidden_delta2.dot(self.w2.T)
        hidden_delta1 = hidden_error1 * sigmoid_derivative(self.a1)

        # 更新权重和偏置
        self.w3 += self.a2.T.dot(output_delta) * learning_rate
        self.b3 += np.sum(output_delta, axis=0, keepdims=True) * learning_rate
        self.w2 += self.a1.T.dot(hidden_delta2) * learning_rate
        self.b2 += np.sum(hidden_delta2, axis=0, keepdims=True) * learning_rate
        self.w1 += X.T.dot(hidden_delta1) * learning_rate
        self.b1 += np.sum(hidden_delta1, axis=0, keepdims=True) * learning_rate

    # 训练模型
    def train(self, X, y, epochs, learning_rate):
        for epoch in range(epochs):
            output = self.forward(X)
            self.backward(X, y, output, learning_rate)
            if epoch % 100 == 0:
                loss = np.mean(np.square(y - output))
                print(f'Epoch {epoch}, Loss: {loss}')

# 示例：训练深度神经网络
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])  # 输入数据
y = np.array([[0], [1], [1], [0]])  # XOR 输出

# 初始化深度神经网络
dnn = DeepNeuralNetwork(input_size=2, hidden_size=4, output_size=1)

# 训练网络
dnn.train(X, y, epochs=10000, learning_rate=0.1)

# 测试结果
output = dnn.forward(X)
print("Predicted Output: n", output)

5.6 深度神经网络的挑战

尽管 DNN 在许多任务中表现出色，但它们的使用也面临诸多挑战：

梯度消失与梯度爆炸：随着网络层数的增加，梯度可能会在反向传播过程中逐渐消失或迅速增长，导致训练过程不稳定。为了解决这些问题，研究人员提出了更深层次的网络架构（如 ResNet），并使用如 ReLU 等激活函数。
计算成本：深度神经网络的训练需要大量的数据和计算资源。通常需要使用 GPU 或分布式计算加速训练过程。
过拟合：DNN 的强大表达能力也意味着它们容易过拟合训练数据，尤其是在数据量不足时。为此，常使用正则化方法（如 Dropout、权重衰减）来减轻过拟合。

5.7 深度神经网络的应用与未来发展

DNN 在各类实际应用中都取得了巨大成功，如图像识别、语音识别、自然语言处理等。然而，随着数据规模和任务复杂度的不断增长，研究人员仍在持续优化网络结构与训练方法，探索更高效的深度学习模型。

应用领域包括：

自动驾驶：DNN 用于识别交通标志、行人、车辆等物体，为自动驾驶系统提供决策依据。
医疗诊断：通过学习大量的医疗图像数据，DNN 可以辅助医生进行疾病诊断，如癌症筛查。
推荐系统：在电子商务和内容推荐领域，DNN 帮助提高推荐的精准度，提升用户体验。

深度神经网络的未来充满了可能性，随着硬件和算法的进步，DNN 的应用领域将不断扩展，并为各行各业带来更多的创新。

6. 常见激活函数

激活函数是深度神经网络中至关重要的组成部分，它决定了神经网络的非线性特性和学习能力。激活函数的主要作用是将神经元的输入信号转换为输出信号，并引入非线性变换，使网络能够学习和拟合复杂的函数映射。

6.1 激活函数的基本作用

在神经网络中，激活函数应用于每个神经元的加权输入之上，产生神经元的输出。其主要作用包括：

引入非线性：线性模型无法处理复杂的非线性关系，而激活函数能够引入非线性，使得神经网络能够处理复杂的数据模式。
增加模型的表达能力：通过适当选择激活函数，可以使网络更好地拟合训练数据，提高模型的表现能力。

6.2 常见的激活函数

以下是一些常见的激活函数及其特点：

6.2.1 Sigmoid 函数

定义：

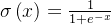
$sigma left ( x right ) = frac{1}{1+e^{-x}}$

特点：

输出范围在 (0, 1) 之间。
适用于二分类任务的输出层。
在深层网络中可能导致梯度消失问题，特别是当输入值很大或很小时。

Python 代码示例：

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# 测试
x = np.array([-2, -1, 0, 1, 2])
print("Sigmoid Output:", sigmoid(x))

6.2.2 ReLU 函数（Rectified Linear Unit）

定义：

特点：

输出范围是 [0, )。
计算简单，能有效缓解梯度消失问题。
可能出现“神经元死亡”现象，即神经元在训练过程中始终输出 0。

Python 代码示例：

def relu(x):
    return np.maximum(0, x)

# 测试
x = np.array([-2, -1, 0, 1, 2])
print("ReLU Output:", relu(x))

6.2.3 Leaky ReLU 函数

定义：

$Leaky ReLUleft ( x right ) =left{begin{matrix} x & if x > 0 \ alpha x &if xleq 0 end{matrix}right.” class=”mathcode” src=””></p> <p>其中，<img decoding=$ 是一个很小的常数（如 0.01）。

特点：

解决了 ReLU 的“神经元死亡”问题，使得负值区域也有微小的梯度。
增加了计算复杂性。

Python 代码示例：

def leaky_relu(x, alpha=0.01):
    return np.where(x > 0, x, alpha * x)

# 测试
x = np.array([-2, -1, 0, 1, 2])
print("Leaky ReLU Output:", leaky_relu(x))

6.2.4 Tanh 函数（双曲正切函数）

定义：

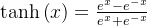
$tanh left ( x right ) = frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}$

特点：

输出范围在 (-1, 1) 之间。
相比于 Sigmoid 函数，Tanh 函数的输出均值为 0，有助于数据标准化。
依然可能出现梯度消失问题。

Python 代码示例：

def tanh(x):
    return np.tanh(x)

# 测试
x = np.array([-2, -1, 0, 1, 2])
print("Tanh Output:", tanh(x))

6.2.5 Softmax 函数

定义：

$Softmaxleft ( x_{i} right ) = frac{e^{x_{i}}}{sum_{j}^{e^{x_{j}}}}$

特点：

将输出转换为概率分布，输出值在 (0, 1) 之间，且总和为 1。
通常用于多分类问题的输出层。

Python 代码示例：

def softmax(x):
    exp_x = np.exp(x - np.max(x))  # 为了数值稳定性
    return exp_x / exp_x.sum(axis=0)

# 测试
x = np.array([2.0, 1.0, 0.1])
print("Softmax Output:", softmax(x))

6.3 激活函数的选择

激活函数的选择对于神经网络的训练和性能有显著影响。以下是一些指导原则：

非线性问题：对于需要捕捉复杂非线性关系的任务，推荐使用 ReLU 或其变种（如 Leaky ReLU）。
输出层：对于二分类任务，通常使用 Sigmoid 函数；对于多分类任务，通常使用 Softmax 函数。
梯度消失：在深层网络中，推荐使用 ReLU 或其变种，以减少梯度消失问题。

6.4 激活函数的未来发展

随着深度学习领域的发展，新的激活函数不断被提出，如 Swish 和 Mish。这些新型激活函数在某些应用场景中表现优于传统函数，未来可能会进一步推动激活函数的研究和应用。

代码示例：Swish 函数

def swish(x):
    return x * sigmoid(x)

# 测试
x = np.array([-2, -1, 0, 1, 2])
print("Swish Output:", swish(x))

总之，选择适当的激活函数是设计神经网络时的重要考虑因素。通过理解不同激活函数的特性和应用场景，可以更有效地设计和优化神经网络，提高模型的性能和训练效率。

7. 优化算法

优化算法在深度学习中扮演着关键角色，它们负责调整神经网络的参数（权重和偏置），以最小化损失函数并提高模型的性能。选择合适的优化算法可以显著提高模型的训练效率和效果。以下是一些常见的优化算法及其详细说明。

7.1 随机梯度下降（SGD）

定义：随机梯度下降（Stochastic Gradient Descent, SGD）是最基本的优化算法。它在每次迭代中使用一个小批量（mini-batch）样本来估计梯度，并更新网络参数。

更新公式：

$theta = theta - eta cdot bigtriangledown _{theta }Jleft ( theta right )$

其中，是模型参数，是学习率， $bigtriangledown _{theta }Jleft ( theta right )$ 是损失函数对的梯度。

优缺点：

优点：简单易实现，适用于大规模数据集。
缺点：在训练过程中，SGD 的更新方向可能受到噪声影响，导致收敛缓慢或不稳定。

Python 代码示例：

import numpy as np

def sgd(parameters, gradients, learning_rate):
    for param, grad in zip(parameters, gradients):
        param -= learning_rate * grad
    return parameters

7.2 动量（Momentum）

定义：动量优化算法通过引入一个“动量”项，来加速 SGD 的收敛速度，并减少梯度下降过程中的振荡现象。

更新公式：

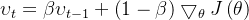
$upsilon_{t} = beta upsilon_{t-1} + left ( 1-beta right )bigtriangledown _{theta }Jleft ( theta right )$

$theta = theta - eta cdot upsilon _{t}$

其中， $upsilon _{t}$ 是动量项，是动量系数，通常设为 0.9。

优缺点：

优点：减少梯度下降的振荡，加速收敛。
缺点：需要调整动量参数。

Python 代码示例：

def momentum(parameters, gradients, velocities, learning_rate, beta):
    for param, grad, velocity in zip(parameters, gradients, velocities):
        velocity = beta * velocity + (1 - beta) * grad
        param -= learning_rate * velocity
    return parameters, velocities

7.3 自适应梯度算法（Adagrad）

定义： Adagrad 算法通过调整每个参数的学习率，使用过去梯度的累积平方和来进行参数更新，能够自适应地调整学习率。

优缺点：

优点：适应性强，对稀疏数据和稀疏特征效果好。
缺点：学习率会随时间单调下降，可能导致收敛缓慢。

Python 代码示例：

def adagrad(parameters, gradients, cache, learning_rate, epsilon=1e-8):
    for param, grad, c in zip(parameters, gradients, cache):
        c += grad**2
        param -= learning_rate * grad / (np.sqrt(c) + epsilon)
    return parameters, cache

7.4 RMSprop

定义： RMSprop 是 Adagrad 的改进版，它使用指数加权平均来计算梯度的平方和，从而避免了学习率过快下降的问题。

优缺点：

优点：适用于非平稳目标和具有不同特征尺度的数据。
缺点：需要选择合适的衰减率参数。

Python 代码示例：

def rmsprop(parameters, gradients, cache, learning_rate, rho=0.9, epsilon=1e-8):
    for param, grad, c in zip(parameters, gradients, cache):
        c = rho * c + (1 - rho) * grad**2
        param -= learning_rate * grad / (np.sqrt(c) + epsilon)
    return parameters, cache

7.5 Adam（Adaptive Moment Estimation）

定义： Adam 是目前使用最广泛的优化算法之一，它结合了动量和 RMSprop 的优点，计算一阶矩（梯度的平均值）和二阶矩（梯度的平方的平均值）来调整学习率。

优缺点：

优点：能够适应学习率，并在多种任务中表现出色。
缺点：需要调节多个超参数。

Python 代码示例：

def adam(parameters, gradients, m, v, t, learning_rate, beta1=0.9, beta2=0.999, epsilon=1e-8):
    for param, grad, m_t, v_t in zip(parameters, gradients, m, v):
        m_t = beta1 * m_t + (1 - beta1) * grad
        v_t = beta2 * v_t + (1 - beta2) * grad**2
        m_hat = m_t / (1 - beta1**t)
        v_hat = v_t / (1 - beta2**t)
        param -= learning_rate * m_hat / (np.sqrt(v_hat) + epsilon)
    return parameters, m, v

7.6 选择优化算法的考虑因素

任务类型：对于大型数据集和复杂任务，Adam 通常是较好的选择，因为它结合了动量和自适应学习率的优点。
计算资源：一些优化算法（如 Adam）可能比 SGD 计算需求更高，需考虑计算资源的限制。
超参数调整：不同的优化算法有不同的超参数（如学习率、动量系数），需要进行适当的调整和优化。

7.7 优化算法的未来发展

优化算法领域在不断发展，新的算法如 LAMB（Layer-wise Adaptive Moments optimizer for Batching training） 和 AdaBelief 等已经在特定应用中表现出色。随着研究的深入和应用的扩展，未来可能会出现更多高效的优化算法，进一步提高深度学习模型的性能和训练效率。

通过理解和掌握这些优化算法，研究人员和工程师可以更有效地训练神经网络模型，从而提升其在各类应用中的表现和鲁棒性。

8. 深度学习框架介绍

深度学习框架是构建和训练神经网络模型的核心工具，它们提供了高效的计算图构建、自动求导、模型训练和评估等功能。选择合适的深度学习框架对于模型开发的效率和效果至关重要。以下是一些主流深度学习框架的详细介绍及其特点。

8.1 TensorFlow

概述： TensorFlow 是由 Google Brain 团队开发的开源深度学习框架，广泛用于研究和生产环境。它支持多种平台，包括 CPU、GPU 和 TPU。

特点：

计算图：TensorFlow 使用静态计算图（定义计算图后再执行）来提高性能。
灵活性：支持多种高级 API（如 Keras）和低级 API。
分布式计算：支持多机多卡训练，适用于大规模数据和模型。

代码示例：以下是一个使用 TensorFlow 构建简单前馈神经网络的代码示例：

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

# 构建模型
model = Sequential([
    Dense(64, activation='relu', input_shape=(784,)),
    Dense(10, activation='softmax')
])

# 编译模型
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

# 假设 X_train 和 y_train 是训练数据和标签
# model.fit(X_train, y_train, epochs=5)

8.2 PyTorch

概述： PyTorch 是由 Facebook 开发的开源深度学习框架，以其动态计算图和易于调试的特性受到研究人员和开发者的欢迎。

特点：

动态计算图：支持即时计算图生成和修改，便于调试和开发。
易于使用：Pythonic 设计，使得编写和理解代码更加直观。
强大的社区支持：活跃的社区和丰富的第三方库支持。

代码示例：以下是一个使用 PyTorch 构建简单前馈神经网络的代码示例：

import torch
import torch.nn as nn
import torch.optim as optim

# 定义模型
class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        self.fc1 = nn.Linear(784, 64)
        self.fc2 = nn.Linear(64, 10)

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = self.fc2(x)
        return x

model = SimpleNN()
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# 假设 train_loader 是训练数据的 DataLoader
# for epoch in range(5):
#     for data, target in train_loader:
#         optimizer.zero_grad()
#         output = model(data)
#         loss = criterion(output, target)
#         loss.backward()
#         optimizer.step()

8.3 Keras

概述： Keras 是一个高级神经网络 API，能够与 TensorFlow、Theano 和 CNTK 后端兼容。它旨在简化模型的构建和训练过程。

特点：

简洁性：设计简洁，易于上手，适合快速原型开发。
易于扩展：可以轻松定义和训练深度学习模型。
集成：与 TensorFlow 紧密集成，是 TensorFlow 2.x 的高级 API 之一。

代码示例：以下是一个使用 Keras 构建简单前馈神经网络的代码示例：

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

# 构建模型
model = Sequential([
    Dense(64, activation='relu', input_shape=(784,)),
    Dense(10, activation='softmax')
])

# 编译模型
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

# 假设 X_train 和 y_train 是训练数据和标签
# model.fit(X_train, y_train, epochs=5)

8.4 MXNet

概述： MXNet 是由 Apache 组织开发的开源深度学习框架，特别适用于高效的分布式训练和跨平台部署。

特点：

高性能：支持高效的分布式训练，适合大规模数据和模型。
灵活性：支持符号式和命令式编程模式。
多语言支持：除了 Python，还支持 R、Scala 和 Julia 等语言。

代码示例：以下是一个使用 MXNet 构建简单前馈神经网络的代码示例：

import mxnet as mx
from mxnet import nd, autograd, gluon

# 定义模型
net = gluon.nn.Sequential()
with net.name_scope():
    net.add(gluon.nn.Dense(64, activation='relu'))
    net.add(gluon.nn.Dense(10))

# 初始化参数
net.initialize()

# 定义损失函数和优化器
softmax_cross_entropy = gluon.loss.SoftmaxCrossEntropyLoss()
trainer = gluon.Trainer(net.collect_params(), 'adam')

# 假设 train_data 是训练数据
# for epoch in range(5):
#     for data, label in train_data:
#         with autograd.record():
#             output = net(data)
#             loss = softmax_cross_entropy(output, label)
#         loss.backward()
#         trainer.step(batch_size)

8.5 Caffe

概述： Caffe 是由伯克利视觉与学习中心（BVLC）开发的深度学习框架，以其高效的计算性能和灵活的配置文件支持受到青睐。

特点：

速度快：优化了卷积神经网络的训练速度。
配置化：通过配置文件定义网络结构和训练参数，便于调整和管理。
可视化：提供了多种工具用于可视化网络结构和训练过程。

代码示例：以下是一个使用 Caffe 进行简单卷积神经网络训练的示例（伪代码）：

# Caffe 通常通过配置文件进行训练，这里展示配置文件内容
# train.prototxt
layer {
  name: "conv1"
  type: "Convolution"
  top: "conv1"
  param { lr_mult: 1 }
  convolution_param {
    num_output: 64
    kernel_size: 3
    stride: 1
  }
}

layer {
  name: "relu1"
  type: "ReLU"
  bottom: "conv1"
  top: "conv1"
}

# 训练过程通常通过 Caffe 的命令行工具进行
# caffe train --solver=solver.prototxt

8.6 深度学习框架的选择考虑因素

性能需求：考虑框架在计算速度、内存管理和分布式训练方面的性能。
易用性：根据框架的 API 设计、文档和社区支持来选择适合自己团队的工具。
平台兼容性：选择支持自己硬件和操作系统的框架。
生态系统：考虑框架的扩展性、第三方库和工具的支持情况。

8.7 未来的发展方向

深度学习框架的发展趋势包括更强的自动化（如 AutoML）、更好的可解释性、对新硬件（如量子计算）的支持以及更加高效的分布式训练机制。新兴框架和技术将不断推动深度学习的研究和应用前沿。

通过掌握这些主流的深度学习框架，研究人员和工程师可以根据具体的应用需求和计算资源，选择最适合的工具进行模型开发和优化，从而提高工作效率和研究成果的质量。

9. 应用案例

深度学习技术在多个领域展现了强大的能力和广泛的应用。以下是一些典型的深度学习应用案例，展示了它们在实际场景中的应用效果和实现方式。

9.1 图像分类

案例概述：图像分类是深度学习最早和最常见的应用之一。通过训练深度神经网络对图像进行分类，可以实现自动标记和识别各种物体和场景。典型的应用包括自动标签、内容过滤和医疗影像分析。

经典模型：

卷积神经网络（CNN）：利用卷积层提取图像特征，通过全连接层进行分类。

Python 代码示例：以下是使用 TensorFlow 和 Keras 实现图像分类的简单示例：

import tensorflow as tf
from tensorflow.keras.datasets import cifar10
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Conv2D, MaxPooling2D, Flatten

# 加载数据
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0  # 数据归一化

# 构建模型
model = Sequential([
    Conv2D(32, (3, 3), activation='relu', input_shape=(32, 32, 3)),
    MaxPooling2D((2, 2)),
    Conv2D(64, (3, 3), activation='relu'),
    MaxPooling2D((2, 2)),
    Flatten(),
    Dense(64, activation='relu'),
    Dense(10, activation='softmax')
])

# 编译模型
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

# 训练模型
model.fit(x_train, y_train, epochs=5, validation_data=(x_test, y_test))

9.2 自然语言处理（NLP）

案例概述：自然语言处理（NLP）涉及对人类语言的理解和生成，应用广泛，包括自动翻译、情感分析、对话系统等。深度学习模型如循环神经网络（RNN）和 Transformer 对 NLP 任务的性能提升具有显著影响。

经典模型：

BERT（Bidirectional Encoder Representations from Transformers）：通过双向编码器来捕捉上下文信息，广泛用于各种 NLP 任务。

Python 代码示例：以下是使用 Hugging Face 的 Transformers 库实现文本分类的简单示例：

from transformers import pipeline

# 创建分类器
classifier = pipeline('sentiment-analysis')

# 使用分类器进行预测
result = classifier("I love using deep learning for natural language processing!")
print(result)

9.3 语音识别

案例概述：语音识别技术通过将语音信号转换为文本，广泛应用于语音助手、自动字幕生成和语音搜索等场景。深度学习方法，如深度神经网络（DNN）和长短时记忆网络（LSTM），在语音识别中具有卓越表现。

经典模型：

Deep Speech：由 Baidu 提出的端到端语音识别模型，使用深度神经网络进行音频到文本的转换。

Python 代码示例：以下是使用 Google 的 SpeechRecognition 库进行语音识别的简单示例：

import speech_recognition as sr

# 初始化识别器
recognizer = sr.Recognizer()

# 加载音频文件
with sr.AudioFile('audio.wav') as source:
    audio = recognizer.record(source)

# 进行语音识别
try:
    text = recognizer.recognize_google(audio)
    print("Recognized text:", text)
except sr.UnknownValueError:
    print("Google Speech Recognition could not understand the audio")
except sr.RequestError:
    print("Could not request results from Google Speech Recognition service")

9.4 自动驾驶

案例概述：自动驾驶技术通过结合图像识别、传感器数据和决策算法来实现车辆的自动驾驶。深度学习在自动驾驶系统中的应用包括车道检测、物体识别和路径规划等。

经典模型：

YOLO（You Only Look Once）：用于实时物体检测的深度学习模型，在自动驾驶中用于检测行人、车辆和障碍物。

Python 代码示例：以下是一个使用 OpenCV 和 YOLO 模型进行实时物体检测的代码示例：

import cv2
import numpy as np

# 加载 YOLO 模型
net = cv2.dnn.readNet('yolov3.weights', 'yolov3.cfg')
layer_names = net.getLayerNames()
output_layers = [layer_names[i[0] - 1] for i in net.getUnconnectedOutLayers()]

# 加载图像
cap = cv2.VideoCapture(0)  # 从摄像头捕获视频

while True:
    ret, frame = cap.read()
    blob = cv2.dnn.blobFromImage(frame, 0.00392, (416, 416), (0, 0, 0), True, crop=False)
    net.setInput(blob)
    outs = net.forward(output_layers)

    # 处理检测结果
    for out in outs:
        for detection in out:
            for obj in detection:
                scores = obj[5:]
                class_id = np.argmax(scores)
                confidence = scores[class_id]
                if confidence > 0.5:
                    # 处理检测到的物体
                    pass

    # 显示图像
    cv2.imshow('Frame', frame)
    if cv2.waitKey(1) & 0xFF == ord('q'):
        break

cap.release()
cv2.destroyAllWindows()

9.5 医疗影像分析

案例概述：医疗影像分析通过自动化的深度学习技术来分析和诊断医疗影像，例如 CT 扫描和 MRI。深度学习可以帮助医生检测异常、预测疾病和制定治疗方案。

经典模型：

U-Net：用于医学图像分割的卷积神经网络模型，具有良好的分割性能。

Python 代码示例：以下是一个使用 Keras 实现 U-Net 模型的简化示例：

import tensorflow as tf
from tensorflow.keras.layers import Input, Conv2D, MaxPooling2D, UpSampling2D, concatenate
from tensorflow.keras.models import Model

def unet_model(input_shape):
    inputs = Input(input_shape)
    c1 = Conv2D(64, (3, 3), activation='relu', padding='same')(inputs)
    c1 = Conv2D(64, (3, 3), activation='relu', padding='same')(c1)
    p1 = MaxPooling2D((2, 2))(c1)
    
    c2 = Conv2D(128, (3, 3), activation='relu', padding='same')(p1)
    c2 = Conv2D(128, (3, 3), activation='relu', padding='same')(c2)
    p2 = MaxPooling2D((2, 2))(c2)
    
    u3 = UpSampling2D((2, 2))(c2)
    u3 = concatenate([u3, c1], axis=3)
    c3 = Conv2D(64, (3, 3), activation='relu', padding='same')(u3)
    c3 = Conv2D(64, (3, 3), activation='relu', padding='same')(c3)
    
    outputs = Conv2D(1, (1, 1), activation='sigmoid')(c3)
    
    model = Model(inputs=[inputs], outputs=[outputs])
    return model

# 构建 U-Net 模型
model = unet_model((128, 128, 1))
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])

9.6 应用案例的总结

这些应用案例展示了深度学习技术在不同领域中的广泛应用和强大能力。通过实际案例的学习，研究人员和工程师可以获取有价值的实践经验，并将这些技术应用于自己的实际问题中。对于每个应用场景，选择合适的模型和方法，并结合实际需求和数据特征进行优化，是实现最佳效果的关键。

掌握这些应用案例不仅能够帮助理解深度学习技术的实际应用，还能为未来的研究和开发提供宝贵的参考和启示。

10. 未来展望与挑战

深度学习技术已经在多个领域取得了显著的进展，但在其发展过程中仍面临诸多挑战。未来的发展方向将涉及模型的复杂性、计算资源的优化、数据隐私的保护以及技术的可解释性等方面。以下是对未来展望与挑战的详细探讨。

10.1 未来展望

1. 模型的可解释性和透明性

随着深度学习模型在关键领域（如医疗、金融等）的应用增加，模型的可解释性变得越来越重要。未来的研究将致力于提高模型的透明性，使其决策过程更加可理解，以便于用户和监管机构进行审查。

技术方向：

可解释性模型：如解释型神经网络（Explainable Neural Networks）和模型可视化技术（如 Grad-CAM）。
模型分析工具：开发更多工具和框架来分析和解释深度学习模型的内部机制。

示例代码（使用 Grad-CAM 可视化模型的特征图）：

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.keras.applications import VGG16
from tensorflow.keras.preprocessing import image
from tensorflow.keras.applications.vgg16 import preprocess_input, decode_predictions

# 加载 VGG16 模型
model = VGG16(weights='imagenet', include_top=True)

# 加载并预处理图像
img_path = 'elephant.jpg'  # 替换为实际图像路径
img = image.load_img(img_path, target_size=(224, 224))
img_array = image.img_to_array(img)
img_array = np.expand_dims(img_array, axis=0)
img_array = preprocess_input(img_array)

# 获取最后一层卷积层的输出
last_conv_layer = model.get_layer('block5_conv3')
heatmap_model = tf.keras.Model([model.inputs], [last_conv_layer.output, model.output])

with tf.GradientTape() as tape:
    conv_outputs, predictions = heatmap_model(img_array)
    loss = predictions[:, np.argmax(predictions[0])]

grads = tape.gradient(loss, conv_outputs)
pooled_grads = tf.reduce_mean(grads, axis=(0, 1, 2))
heatmap = tf.reduce_mean(tf.multiply(pooled_grads, conv_outputs), axis=-1)[0]
heatmap = tf.maximum(heatmap, 0) / tf.max(heatmap)
heatmap = np.uint8(255 * heatmap)

plt.matshow(heatmap)
plt.show()

2. 自适应学习算法

未来的研究将专注于开发更加高效和自适应的学习算法，以提高模型的训练效率和性能。这包括智能优化算法、自动化机器学习（AutoML）技术等。

技术方向：

自适应优化器：如 AdamW、LAMB 等。
AutoML：自动化模型选择和超参数调优技术。

示例代码（使用 AutoKeras 进行自动化模型搜索）：

import autokeras as ak
import tensorflow as tf
from tensorflow.keras.datasets import cifar10

# 加载数据
(x_train, y_train), (x_test, y_test) = cifar10.load_data()

# 构建 AutoKeras 图像分类模型
clf = ak.ImageClassifier(max_trials=10)
clf.fit(x_train, y_train, epochs=10)

# 评估模型
accuracy = clf.evaluate(x_test, y_test)
print("Test accuracy: {:.2f}%".format(accuracy[1] * 100))

3. 跨模态学习

跨模态学习将多种数据模态（如图像、文本、语音等）融合在一起，提升模型的理解能力和应用广度。未来的研究将进一步探索如何有效地结合这些信息源。

技术方向：

多模态学习模型：如 CLIP（Contrastive Language-Image Pretraining）模型。
数据融合技术：研究如何处理和融合来自不同来源的数据。

示例代码（使用 CLIP 进行图像-文本匹配）：

from transformers import CLIPProcessor, CLIPModel
from PIL import Image

# 加载模型和处理器
model = CLIPModel.from_pretrained("openai/clip-vit-base-patch32")
processor = CLIPProcessor.from_pretrained("openai/clip-vit-base-patch32")

# 加载和处理图像
image = Image.open('image.jpg')  # 替换为实际图像路径
inputs = processor(text=["a photo of a cat", "a photo of a dog"], images=image, return_tensors="pt", padding=True)

# 获取模型输出
outputs = model(**inputs)
logits_per_image = outputs.logits_per_image  # 图像-文本匹配分数
probs = logits_per_image.softmax(dim=1)  # 计算概率
print(probs)

10.2 挑战

1. 数据隐私和安全

随着数据隐私法规的日益严格，如 GDPR 和 CCPA，如何在保护用户隐私的同时有效使用数据，是深度学习应用中的一大挑战。隐私保护技术（如差分隐私）将成为研究重点。

技术方向：

差分隐私：通过添加噪声保护数据隐私。
联邦学习：在分布式环境中训练模型，避免直接访问用户数据。

示例代码（使用 PySyft 实现联邦学习）：

import syft as sy
import torch
from torch import nn, optim

# 创建虚拟数据
hook = sy.TorchHook(torch)
federated_train_loader = sy.FederatedDataLoader(federated_train_data, batch_size=64)

# 创建模型
model = nn.Sequential(nn.Linear(784, 128), nn.ReLU(), nn.Linear(128, 10))

# 训练模型
optimizer = optim.SGD(model.parameters(), lr=0.1)
criterion = nn.CrossEntropyLoss()

for epoch in range(5):
    for batch in federated_train_loader:
        model.send(batch.location)
        optimizer.zero_grad()
        output = model(batch.data)
        loss = criterion(output, batch.target)
        loss.backward()
        optimizer.step()
        model.get()

2. 计算资源和效率

深度学习模型越来越复杂，对计算资源的需求也随之增加。未来的研究将聚焦于如何优化计算资源，减少训练时间和成本，包括模型压缩和加速技术。

技术方向：

模型压缩：如剪枝、量化和知识蒸馏。
高效硬件：如专用集成电路（ASICs）和图形处理单元（GPUs）优化。

示例代码（使用 TensorFlow 模型压缩 API）：

import tensorflow as tf
from tensorflow_model_optimization.sparsity import keras as sparsity

# 构建模型
model = tf.keras.Sequential([
    tf.keras.layers.Dense(128, activation='relu'),
    tf.keras.layers.Dense(10)
])

# 定义模型压缩策略
pruning_params = {
    'pruning_schedule': sparsity.PolynomialDecay(initial_sparsity=0.0,
                                                final_sparsity=0.5,
                                                begin_step=2000,
                                                end_step=4000)
}

pruned_model = sparsity.prune_low_magnitude(model, **pruning_params)
pruned_model.compile(optimizer='adam',
                     loss='sparse_categorical_crossentropy',
                     metrics=['accuracy'])

# 训练模型
pruned_model.fit(x_train, y_train, epochs=5)

3. 模型的鲁棒性和公平性

深度学习模型可能受到 adversarial attacks 的威胁，这些攻击旨在扰乱模型的预测。此外，模型的公平性问题也日益受到关注，如偏见和歧视。未来的研究将致力于提高模型的鲁棒性和公平性。

技术方向：

对抗训练：通过生成对抗样本来提高模型的鲁棒性。
公平性检测：评估和纠正模型中的偏见和歧视。

示例代码（使用 CleverHans 进行对抗攻击）：

import tensorflow as tf
import tensorflow_addons as tfa
from cleverhans.tf2.attacks import fast_gradient_method

# 构建模型
model = tf.keras.Sequential([
    tf.keras.layers.Dense(128, activation='relu'),
    tf.keras.layers.Dense(10)
])

# 创建对抗样本
def create_adversarial_example(image, label):
    with tf.GradientTape() as tape:
        tape.watch(image)
        prediction = model(image)
        loss = tf.keras.losses.sparse_categorical_crossentropy(label, prediction)
    gradient = tape.gradient(loss, image)
    adversarial_example = fast_gradient_method(model, image, eps=0.1, norm=np.inf)
    return adversarial_example

# 生成对抗样本
adversarial_image = create_adversarial_example(x_test[0:1], y_test[0:1])

未来深度学习的发展将会集中在技术优化和应用拓展上。解决当前面临的挑战，例如数据隐私、计算资源、模型鲁棒性和公平性，将对深度学习的广泛应用和持续发展起到关键作用。研究人员和工程师需要持续关注这些领域的最新进展，并积极探索创新解决方案，以推动深度学习技术向更高水平发展。

通过深入理解和应对这些挑战，行业从业者不仅能提高深度学习技术的应用效果，还能为社会带来更大价值。在不断变化的技术环境中，保持对新技术和新挑战的敏感性，是推动行业进步的关键。

11. 总结

深度学习作为机器学习的一个重要分支，已经在众多领域取得了显著的进展。从图像识别到自然语言处理，深度学习技术的应用不断推动着科技和产业的发展。本篇文章对深度学习的核心概念、关键技术、应用案例以及未来展望进行了详细的探讨。以下是对文章内容的总结和行业借鉴意义的提炼。

11.1 深度学习的核心概念

深度学习是基于人工神经网络的一个子领域，通过多层次的网络结构自动从数据中提取特征和模式。其核心在于通过层层非线性变换，能够处理复杂的输入数据，提升模型的表达能力和预测精度。本文深入探讨了以下关键概念：

神经网络结构：包括前馈神经网络（FNN）和深度神经网络（DNN），以及它们如何通过层叠的方式增强模型的特征学习能力。
激活函数：如ReLU、Sigmoid、Tanh等，激活函数在神经网络中起着至关重要的作用，它们引入非线性因素，使模型能够学习复杂的模式。
优化算法：如梯度下降、Adam优化器等，用于调整模型参数以最小化损失函数，提高模型的训练效果。
深度学习框架：TensorFlow、PyTorch、Keras等框架提供了高效的工具和库，帮助研究人员和工程师构建和训练深度学习模型。

11.2 反向传播与梯度下降

反向传播算法通过计算损失函数关于各层参数的梯度来更新网络权重，是深度学习中关键的训练机制。梯度下降优化算法则通过调整参数以最小化损失函数，从而提升模型性能。本文中详细介绍了这些算法的原理及其实现方法，并附带了示例代码来展示如何在实际应用中使用这些算法。

import numpy as np

# 定义损失函数
def loss_function(y_true, y_pred):
    return np.mean((y_true - y_pred) ** 2)

# 定义梯度下降算法
def gradient_descent(x, y, learning_rate=0.01, epochs=100):
    m = len(y)
    theta = np.zeros(x.shape[1])
    for _ in range(epochs):
        predictions = x.dot(theta)
        errors = predictions - y
        gradients = (2/m) * x.T.dot(errors)
        theta -= learning_rate * gradients
    return theta

11.3 深度学习框架与工具

深度学习框架如TensorFlow、PyTorch和Keras为模型的构建、训练和评估提供了强大的支持。选择适当的框架可以显著提升开发效率和模型性能。本文中介绍了每种框架的特点及其适用场景，并提供了基本的示例代码，帮助读者快速上手。

import torch
import torch.nn as nn
import torch.optim as optim

# 定义简单的神经网络模型
class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        self.fc1 = nn.Linear(784, 128)
        self.fc2 = nn.Linear(128, 10)
    
    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = self.fc2(x)
        return x

model = SimpleNN()
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# 训练过程的简化示例
def train_model(model, data_loader, criterion, optimizer, epochs=5):
    for epoch in range(epochs):
        for inputs, labels in data_loader:
            optimizer.zero_grad()
            outputs = model(inputs)
            loss = criterion(outputs, labels)
            loss.backward()
            optimizer.step()

11.4 未来展望与挑战

深度学习技术的未来发展将集中在提高模型的可解释性、处理数据隐私问题、优化计算资源使用以及应对模型的鲁棒性和公平性等方面。行业在这些方面的探索将直接影响深度学习技术的实际应用效果和社会影响。本文总结了这些挑战，并提出了一些应对策略和研究方向。

11.5 行业借鉴与学习

对于行业从业者和研究人员来说，深入了解深度学习的基本概念和技术、掌握相关的工具和框架、关注最新的技术发展和应用趋势，是推动技术进步和创新的关键。本文提供的示例代码和实际应用案例，能够帮助读者更好地理解和应用深度学习技术。

通过系统地学习和实践深度学习技术，行业从业者不仅能够提升自己的技术能力，还能够为行业带来更多创新解决方案。在不断发展的技术环境中，保持对新技术的敏感性和对挑战的应对能力，是取得成功的关键。

总结来说，深度学习作为一个不断进步的领域，拥有巨大的潜力和应用前景。通过持续的研究和实践，我们可以不断突破技术瓶颈，推动深度学习技术在更多领域发挥作用，实现更大的社会和经济价值。

12. 参考资料

在深入研究和应用深度学习的过程中，参考相关的文献、教程和工具是非常重要的。以下是一些关键的参考资料，包括经典的书籍、重要的论文、知名的深度学习框架以及在线资源。这些资源可以帮助研究人员和工程师更好地理解深度学习的理论与实践，并获得最新的技术发展信息。

12.1 经典书籍

《深度学习》 (Deep Learning)
- 作者: Ian Goodfellow, Yoshua Bengio, 和 Aaron Courville
- 介绍: 这本书是深度学习领域的权威著作，涵盖了从基本理论到前沿技术的广泛内容。适合希望深入了解深度学习原理和技术的读者。
- 链接: Deep Learning Book
《神经网络与深度学习》 (Neural Networks and Deep Learning)
- 作者: Michael Nielsen
- 介绍: 这是一本在线免费书籍，适合深度学习初学者，详细解释了神经网络的基本概念和深度学习的应用。
- 链接: Neural Networks and Deep Learning
《Pattern Recognition and Machine Learning》
- 作者: Christopher M. Bishop
- 介绍: 这本书提供了关于模式识别和机器学习的详细理论基础，适合那些希望深入理解机器学习算法的人。
- 链接: Pattern Recognition and Machine Learning

12.2 重要论文

“ImageNet Classification with Deep Convolutional Neural Networks”
- 作者: Alex Krizhevsky, Ilya Sutskever, 和 Geoffrey Hinton
- 介绍: 这篇论文介绍了AlexNet模型，它在ImageNet竞赛中取得了突破性成果，推动了卷积神经网络的发展。
- 链接: AlexNet Paper
“Deep Residual Learning for Image Recognition”
- 作者: Kaiming He, Xiangyu Zhang, Shaoqing Ren, 和 Jian Sun
- 介绍: 这篇论文提出了ResNet模型，通过引入残差连接解决了深层网络训练中的退化问题。
- 链接: ResNet Paper
“Attention is All You Need”
- 作者: Ashish Vaswani, Noam Shazeer, Niki Parmar, et al.
- 介绍: 论文提出了Transformer模型，彻底改变了自然语言处理领域。
- 链接: Transformer Paper

12.3 知名深度学习框架

TensorFlow
- 开发者: Google
- 介绍: TensorFlow 是一个开源深度学习框架，支持大规模的机器学习和深度学习模型的构建与训练。
- 链接: TensorFlow 官网
PyTorch
- 开发者: Facebook
- 介绍: PyTorch 是一个开源深度学习框架，以其动态图计算和灵活性著称，广泛用于学术研究和工业应用。
- 链接: PyTorch 官网
Keras
- 开发者: François Chollet
- 介绍: Keras 是一个高级深度学习 API，简化了 TensorFlow 和其他后端框架的模型构建过程。
- 链接: Keras 官网

12.4 在线资源与教程

Coursera 深度学习专项课程
- 讲师: Andrew Ng
- 介绍: 该课程涵盖了深度学习的基础知识和应用，包括神经网络、卷积神经网络、序列模型等。
- 链接: Coursera 深度学习专项课程
Fast.ai 深度学习课程
- 讲师: Jeremy Howard 和 Rachel Thomas
- 介绍: Fast.ai 提供的课程旨在使深度学习更加容易上手，并提供了实用的编程练习。
- 链接: Fast.ai 深度学习课程
Google AI 教育资源
- 介绍: Google 提供了一系列的深度学习教育资源，包括教程、课程和案例研究。
- 链接: Google AI 教育
Kaggle 数据科学竞赛平台
- 介绍: Kaggle 提供了丰富的数据集和竞赛平台，适合进行深度学习项目的实战训练。
- 链接: Kaggle 官网

通过参考这些经典书籍、重要论文和开源资源，研究人员和工程师可以获得全面的深度学习知识和实践经验。这些资源不仅能够提供深度学习技术的理论基础，还能帮助在实际项目中应用和优化模型，推动深度学习技术的进一步发展和应用。

这篇文章旨在帮助读者从零开始理解深度学习的基本原理，并通过案例和代码示例，提供了一个完整的入门框架。在实际应用中，读者可以根据具体任务选择合适的网络架构与优化算法，进一步深入探索深度学习的广阔领域。

声明：本站所有文章，如无特殊说明或标注，均为本站原创发布。任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益，可联系我们进行处理。