目录
1、DFS算法简介
DFS,全称为 Depth First Traversal,深度优先遍历。
DFS算法是在树或者图这样的数据结构中常用的一种遍历算法。这个算法会尽可能深的搜索树或者图的分支,直到⼀条路径上的所有节点都被遍历完毕,然后再回溯到上一层,继续寻找另外一条路遍历。
简单来说,DFS就是:优先考虑深度,换句话说就是一条路走到黑,直到无路可走的情况下,才会选择回头,然后重新选择一条路。
在二叉树中,常见的深度优先遍历有:前序遍历、中序遍历以及后序遍历。
2、算法实战应用【leetcode】
2.1 计算布尔二叉树的值
2.1.1 算法原理
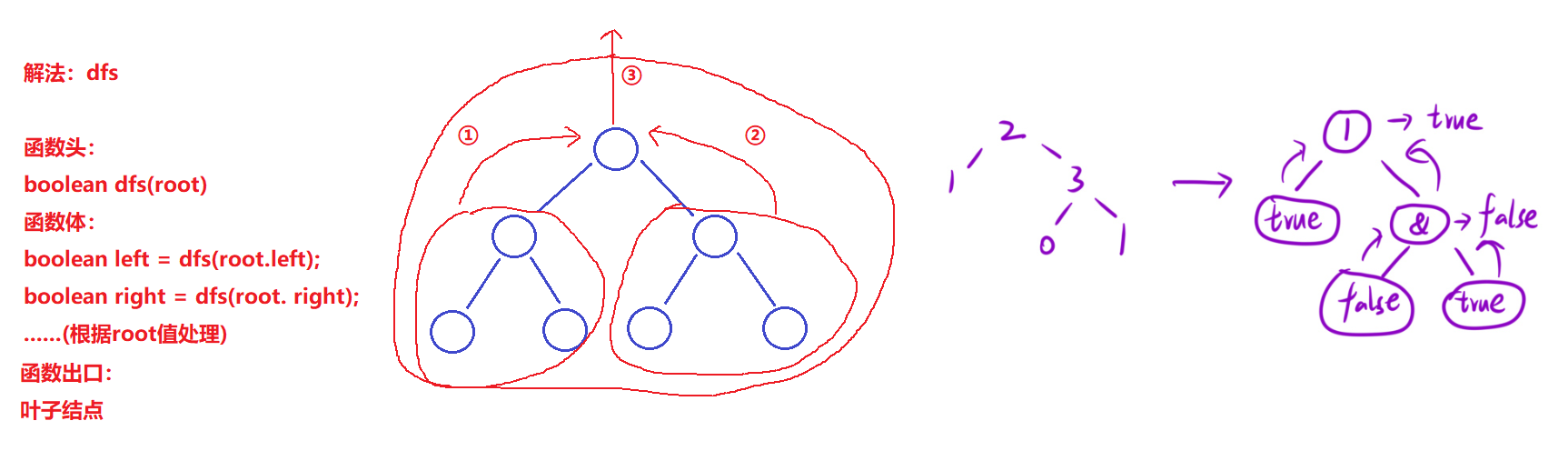
- 以宏观角度看待递归
- 后序遍历拿到最终值
- 函数头:boolean dfs(root);
- 宏观思想–>函数体:返回左子树的布尔值,返回右子树的布尔值,根据当前根节点返回最终结果
- 函数出口:叶子节点,根据叶子节点数值返回布尔类型值
2.1.2 算法代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean evaluateTree(TreeNode root) {
if(root.left == null)
return root.val == 0 ? false : true;
boolean left = evaluateTree(root.left);
boolean right = evaluateTree(root.right);
return root.val == 2 ? left || right : left && right;
}
}2.2 求根节点到叶节点数字之和
2.2.1 算法原理
- 递归的过程中,我们需要传递上层以及本层节点数字之和preSum
- 将上层以及本层节点数字之和preSum传递给当前根节点的左右子树
- 返回左右子树数值之和
- 函数出口:叶子节点。注意:要先将叶子节点的数值注入总和之中再返回
 2.2.2 算法代码
2.2.2 算法代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int sumNumbers(TreeNode root) {
return dfs(root, 0);
}
public int dfs(TreeNode root, int preSum) {
preSum = preSum * 10 + root.val;
if(root.left == null && root.right == null) return preSum;
int ret = 0;
//剪枝
if(root.left != null) ret += dfs(root.left, preSum);
if(root.right != null) ret += dfs(root.right, preSum);
return ret;
}
}2.3 二叉树剪枝
2.3.1 算法原理
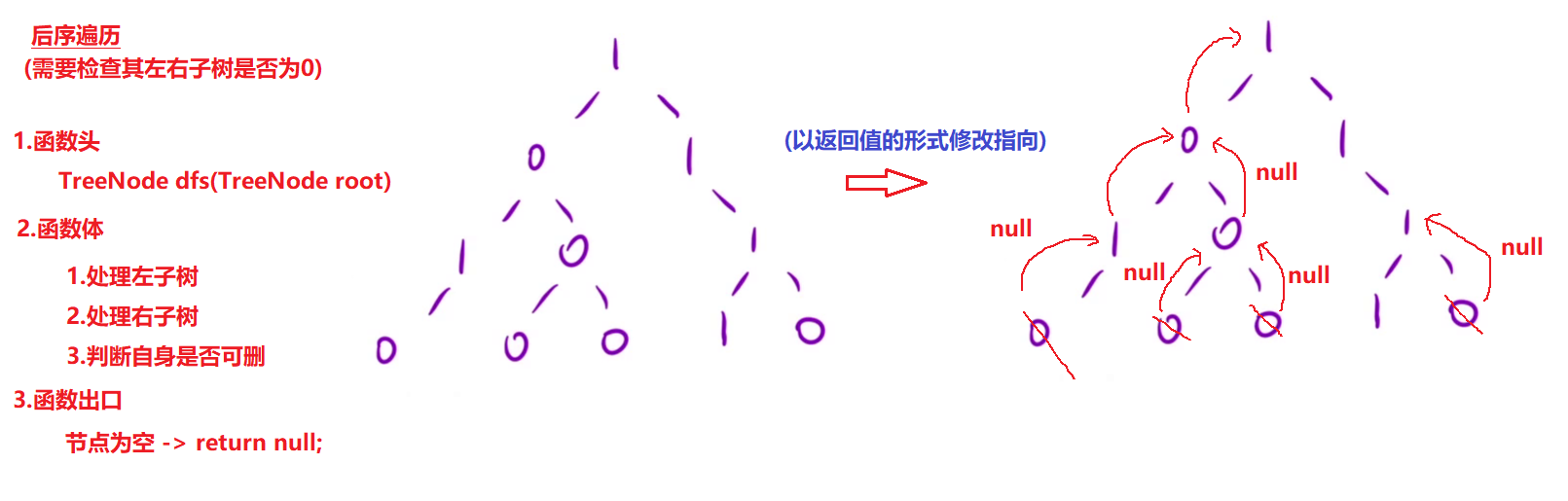
- 思想:后序遍历,当根节点的左右子树的所有值均为0时,才可删除当前树
- 从叶子节点开始判断,若其值为0则可删除
- 可被删除的节点返回null,父节点.left/right接收null,修改其父节点的指向
- 继续判断当前节点
2.3.2 算法代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode pruneTree(TreeNode root) {
if(root == null) return null;
root.left = pruneTree(root.left);
root.right = pruneTree(root.right);
if(root.left == null && root.right == null && root.val == 0) return null;
else return root;
}
}2.4 验证二叉搜索树
2.4.1 算法原理
本题所用思想:
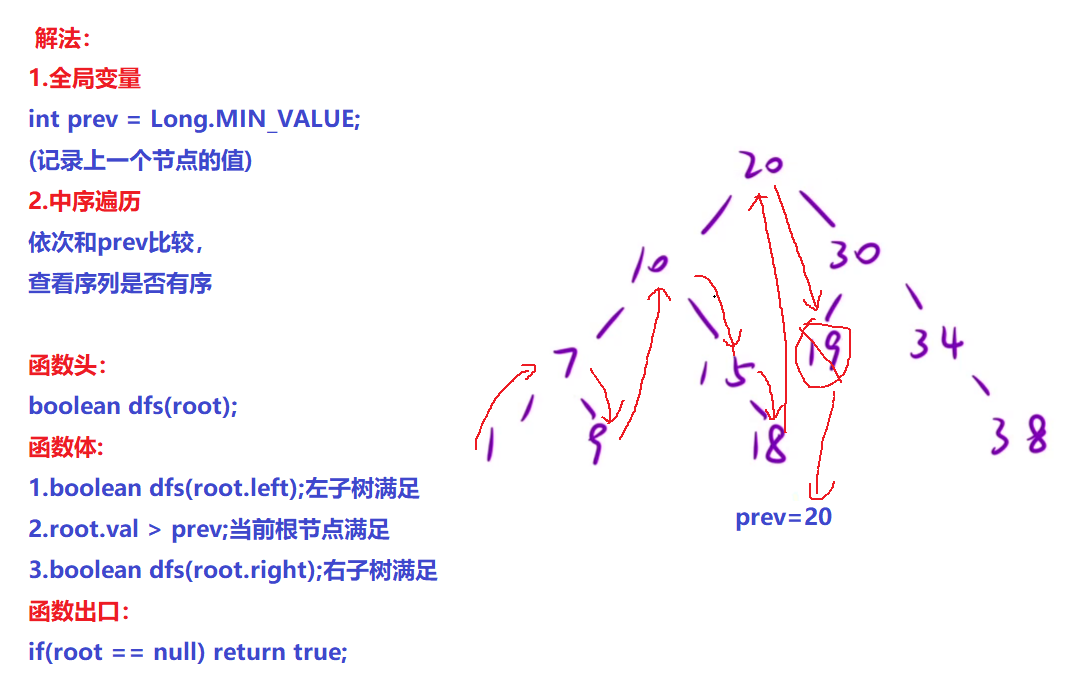
- 全局变量 int prev = Long.MIN_VALUE;(记录上一个节点的值)
- 中序遍历(将当前根节点依次和prev比较,查看序列是否有序)
- 需当前节点的左子树与右子树均满足二叉搜索树,以及当前节点本身满足二叉搜索树,才能说明该树为二叉搜索树
- 若当前节点满足,则更新prev的值为当前节点的val值;若当前节点不满足,则返回false,再通过剪枝优化代码,使函数提前终止并返回false。
2.4.2 算法代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
long prev = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
if(root == null) return true;
boolean left = isValidBST(root.left);
if(prev >= root.val) {
return false;
}
prev = root.val;
boolean right = isValidBST(root.right);
return left && right;
}
}2.5 二叉搜索树中第K小的元素
2.5.1 算法原理
与上一题思想一致,因为是二叉搜索树,所以中序遍历是突破口:
- 设置两个全局变量:public int count+public int ret
- 中序遍历(通过有序序列查找目标值)
- 因为中序遍历得到的是一个有序序列,所以利用count计数,计到第k个数时,使用ret存入
- 得到目标值后,在通过剪枝优化函数,使递归返回

2.5.2 算法代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int count;
public int ret;
public int kthSmallest(TreeNode root, int k) {
count = k;
dfs(root);
return ret;
}
public void dfs(TreeNode root) {
//count == 0 -> 剪枝
if(root == null || count == 0) return;
dfs(root.left);
count--;
if(count == 0) {
ret = root.val;
//剪枝
return;
}
dfs(root.right);
}
}2.6 二叉树的所有路径
2.6.1 算法原理
本题使用思想:
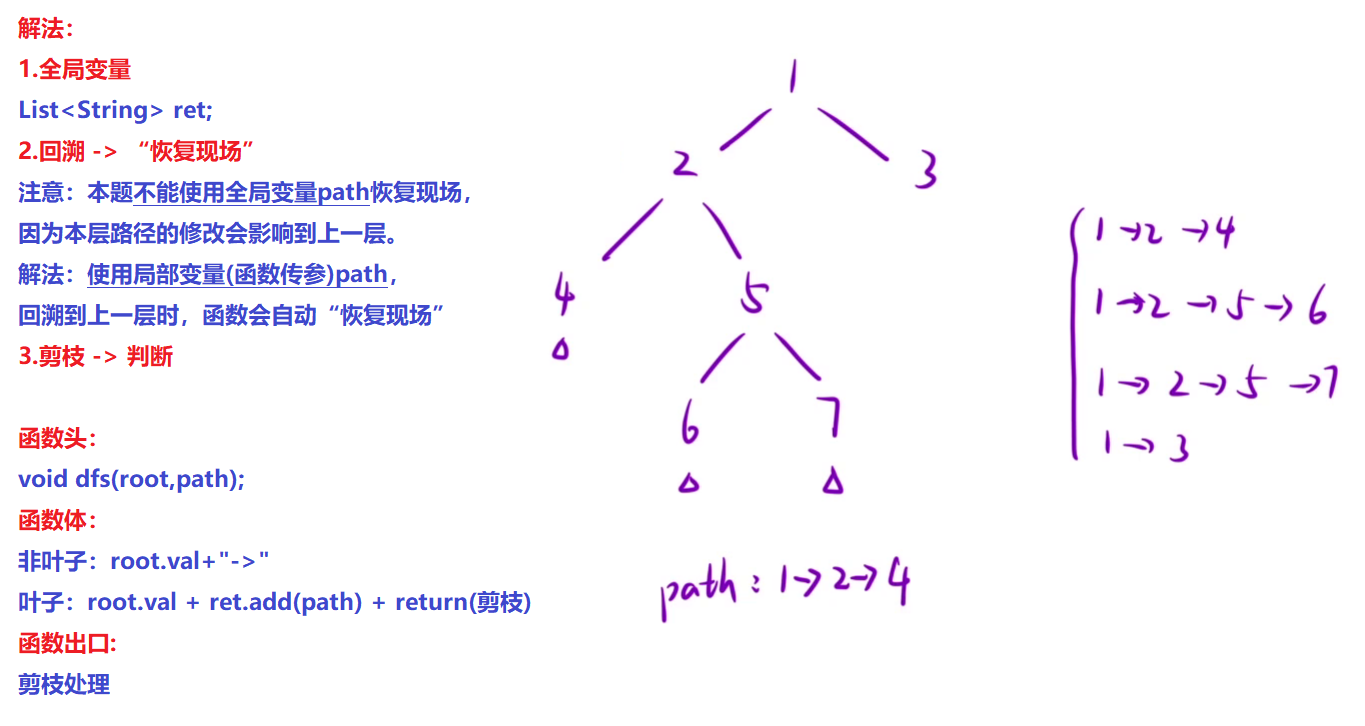
- 设置全局变量:List
ret; - 回溯 -> “恢复现场”
- 注意:本题不能使用全局变量path恢复现场,因为本层路径的修改会影响到上一层。解法:使用局部变量(函数传参)path,回溯到上一层时,函数会自动“恢复现场”。
- 剪枝 -> 优化代码
函数设计:
- 函数头:void dfs(root,path);
- 函数体:非叶子:root.val+”->” ;叶子:root.val + ret.add(path) + return(剪枝)
- 函数出口 -> 剪枝处理
 2.6.2 算法代码
2.6.2 算法代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List ret = new ArrayList();
public List binaryTreePaths(TreeNode root) {
//path -> 记录路径
//回溯 -> 函数自动“恢复现场”
dfs(root, new StringBuffer());
return ret;
}
public void dfs(TreeNode root, StringBuffer path_) {
//保留上一层路径
StringBuffer path = new StringBuffer(path_);
path.append(root.val);
if(root.left == null && root.right == null) {
ret.add(path.toString());
return;
}
path.append("->");
//if -> 剪枝,省略函数出口
if(root.left != null) dfs(root.left, path);
if(root.right != null) dfs(root.right, path);
}
} END
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。

评论(0)