1. 神经网络
构建一个神经网络步骤如下:
-
- 构建一个神经网络
-
- 构造一个学习函数
F
(
x
,
v
)
F(x,v)
F(x,v),x代表权重A
k
,
b
k
A_k,b_k
Ak,bk,v代表样本特征向量,ReLu激活函数
v
1
=
R
e
L
u
[
F
(
A
1
,
b
1
,
v
0
)
]
→
v
1
=
R
e
L
u
[
A
1
v
0
+
b
1
]
begin{equation} v_1=mathrm{ReLu}[F(A_1,b_1,v_0)]to v_1=mathrm{ReLu}[A_1v_0+b_1] end{equation}
v1=ReLu[F(A1,b1,v0)]→v1=ReLu[A1v0+b1]
- 构造一个学习函数
-
- 不断循环迭代上诉公式,构建神经网络
v
k
=
R
e
L
u
[
A
k
v
k
−
1
+
b
k
]
begin{equation} v_{k}=mathrm{ReLu}[A_{k}v_{k-1}+b_{k}] end{equation}
vk=ReLu[Akvk−1+bk]
- 不断循环迭代上诉公式,构建神经网络
- 神经网络图如下:
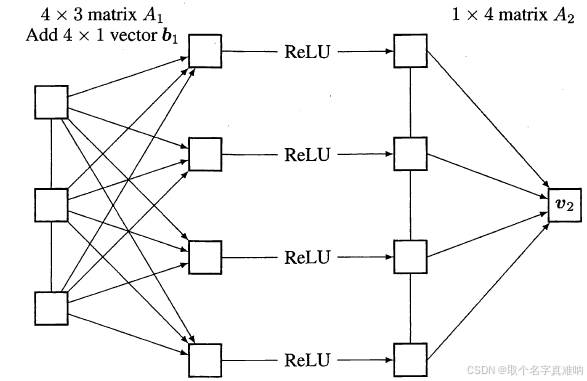
2. 损失函数
神经网络损失函数如下:
L
(
x
)
=
{
1
N
∑
i
=
1
N
[
F
(
x
,
x
i
)
−
t
r
u
e
i
]
2
}
begin{equation} L(x)={frac{1}{N}sum_{i=1}^N[F(x,x_i)-true_i]^2} end{equation}
L(x)={N1i=1∑N[F(x,xi)−truei]2}
- 常见的损失函数如下:
– 最小平方损失函数
– L1范数损失函数
– 交叉熵损失函数
– Hinge损失函数
3. 距离矩阵
假设我们有两个点
x
i
,
x
j
x_i,x_j
xi,xj,用D表示点之间的距离如下:
d
i
j
=
∣
∣
x
i
−
x
j
∣
∣
2
2
begin{equation} d_{ij}=||x_i-x_j||_2^2 end{equation}
dij=∣∣xi−xj∣∣22
- 距离向量化分解:
d
i
j
=
∣
∣
x
i
−
x
j
∣
∣
2
=
(
x
i
−
x
j
)
T
(
x
i
−
x
j
)
=
x
i
T
x
i
−
x
i
T
x
j
−
x
j
T
x
i
+
x
j
T
x
j
begin{equation} d_{ij}=||x_i-x_j||^2=(x_i-x_j)^T(x_i-x_j)=x_i^Tx_i-x_i^Tx_j-x_j^Tx_i+x_j^Tx_j end{equation}
dij=∣∣xi−xj∣∣2=(xi−xj)T(xi−xj)=xiTxi−xiTxj−xjTxi+xjTxj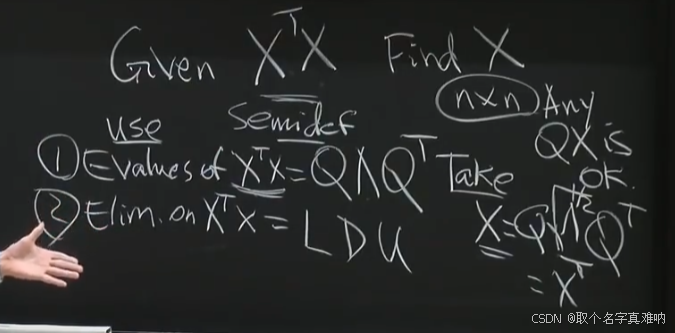

评论(0)