Tips:本文为理解神经网络的前置知识,整体内容并不全,相关内容还需后续进一步完善。
一、基础
1、标量、向量和矩阵
标量:只有大小,没有方向的量
向量(欧几里得向量):具有大小和方向的量。
矩阵:按照长方阵列排列的复数或实数集合
数学中的表示:
2、布局引入
2.1、标量对标量的导数
高等数学里面,我们已经学过了标量对标量求导,如下

有时候可能会有两个自变量,:
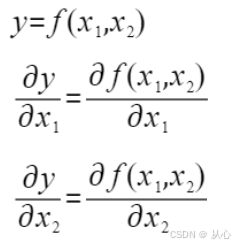
2.2、标量对向量的导数
我们将上面的两个标量写成向量形式,于是有(标量 y ,向量 x ):
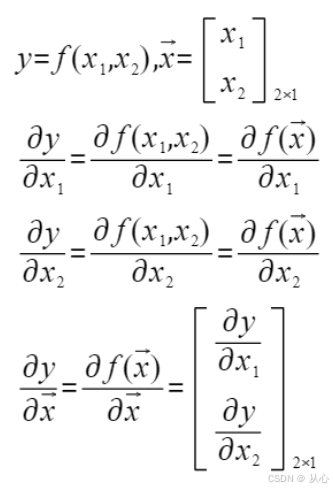
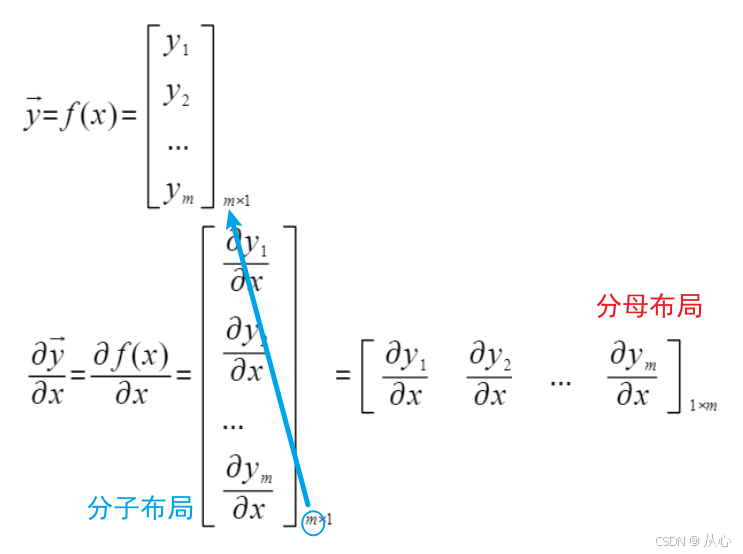
将两个推广到多个,就有了标量对向量求导的形式:

那么问题来了,一个标量y对维度为m的向量x求导,那么结果也是一个m维的向量,那么这个结果向量是行向量,还是列向量呢?
可见标量对向量的求导,就是标量对向量中每个分量求导,最后把他们排列在一起,按一个向量表示,同理也可以得到向量对标量的求导、向量对向量的求导、标量对矩阵的求导、矩阵对标量的求导、向量对矩阵的求导、矩阵对向量的求导、矩阵对矩阵的求导。

如上,标量y对维度为m的一个向量x 的求导,那么结果也是一个m维的向量。这个m维的求导结果排列成的m维列向量或行向量均可。
但在我们机器学习算法法优化过程中,如果行向量或者列向量随便写,那么结果就不唯一,为了解决这个问题,我们引入求导布局的概念。
3、分子布局(numerator layout)和分母布局(denominator layout)
3.1、标量对向量的求导
对于分子布局,我们求导结果的维度以分子为主,比如上面标量对向量求导的例子,结果的维度和分子的维度是一致的。也就是说,如果向量x是一个m维的行向量,那么求导结果是一个m维列向量。如果向量x是一个m维列向量,那么求导结果是一个m维行向量。
对于分母布局来说,我们求导结果的维度以分母为主,如果向量x是一个m维的行向量,那么求导结果也是一个m维行向量。如果向量x是一个m维的列向量,那么求导结果也是一个m维的列向量。
分子布局和分母布局的结果来说,两者互为转置。

3.2、向量对标量的求导
同理可得:
3.4、向量对向量的求导
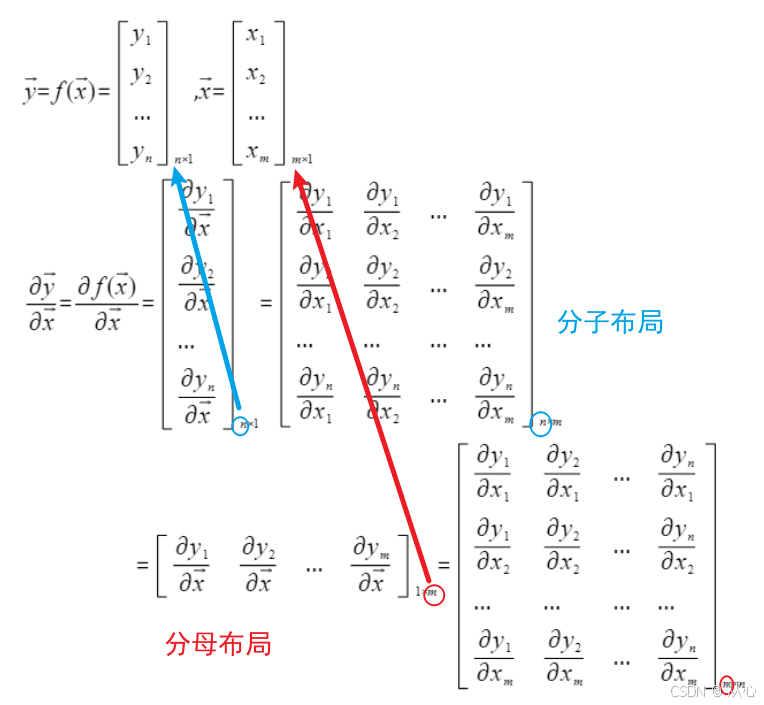
3.5、标量对矩阵的求导
标量y对矩阵X(m*n)求导:
- 分子布局:求导结果维度为n*m
- 分母布局:求导结果维度与分母的矩阵X维度一致,为m*n
3.6、矩阵对标量的求导
矩阵Y(m*n)对标量x求导:
- 分子布局:求导结果维度与分子的矩阵Y维度一致,为m*n
- 分母布局:求导结果为n*m
向量对矩阵的求导、矩阵对向量的求导、矩阵对矩阵的求导。

评论(0)