2024 年高教社杯全国大学生数学建模竞赛题目【A/B/C/D/E题】完整思路

↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑

A题是数模类赛事很常见的物理类赛题，需要学习不少相关知识。此题涉及对一个动态系统的建模，模拟一支舞龙队伍在螺旋路径中的行进，并求解队伍的整体动态行为。包括队伍的每秒位置、速度、碰撞检测、路径优化等问题。

这道题目主要涉及复杂的几何建模和动态模拟。队伍的行进路径需要通过螺旋曲线建模，且动态参数（速度、位置等）需要精确计算并避免碰撞。问题的限制条件较为明确，开放性一般，适合擅长几何建模和动力学仿真的同学。也就是物理学等相关专业的同学进行选择。在其中还涉及到了微分方程求解以及碰撞检测算法

这道题专业性较高，后续账号会在出本题具体思路分析时，再进行具体分析与建模。开放程度低，难度适中。但这类赛题通常门槛较高，小白/非相关专业同学谨慎选择。建议在最后对对答案，答案的正确与否会对最终成绩产生较大影响。建议物理、电气、自动化等相关专业选择。

问题 1

舞龙队沿螺距为 55 cm 的等距螺线顺时针盘入，给出从初始时刻到 300 s 为止，每秒整个舞龙队的位置和速度。

舞龙队沿螺距为55 cm的等距螺线顺时针盘入，各把手中心均位于螺线上。龙头前把手的行进速度始终保持1m/s。初始时，龙头位于螺线第16圈A点处（见图4）。请给出从初始时刻到300s为止，每秒整个舞龙队的位置和速度（指龙头、龙身和龙尾各前把手及龙尾后把手中心的位置和速度，下同），将结果保存到文件result1.xlsx中（模板文件见附件，其中“龙尾（后）”表示龙尾后把手，其余的均是前把手，结果保留6位小数，下同）。同时在论文中给出0 s、60 s、120 s、180 s、240 s、300 s 时，龙头前把手、龙头后面第1、51、101、151、201节龙身前把手和龙尾后把手的位置和速度（格式见表1和表2）。

解题思路：

1.建立螺线方程：螺线的极坐标方程为 r=a+bθr=a+bθ，其中 aa 和 bb 是常数，θθ 是角度。已知螺距为 55 cm，可以确定 bb。

2.初始位置：龙头初始位于螺线第 16 圈 A 点处，计算初始位置的极坐标 (r0,θ0)(r0,θ0)。

3.龙头运动：龙头前把手的行进速度为 1 m/s，计算每秒龙头的位置 (rt,θt)(rt,θt)。

4.龙身和龙尾：根据龙头的位置和速度，计算每节龙身和龙尾的位置和速度。注意板凳的长度和连接方式。

5.数据存储：将每秒的位置和速度数据保存到文件 result1.xlsx 中，并在论文中给出特定时刻的数据。

…………………………………………..

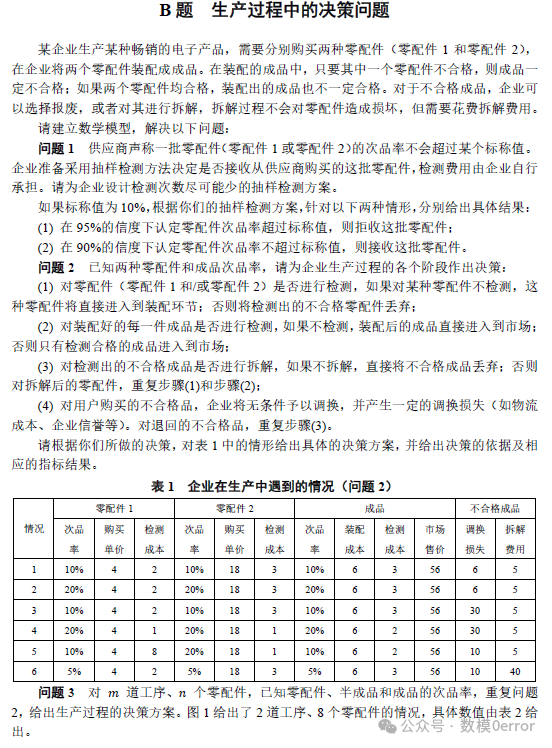
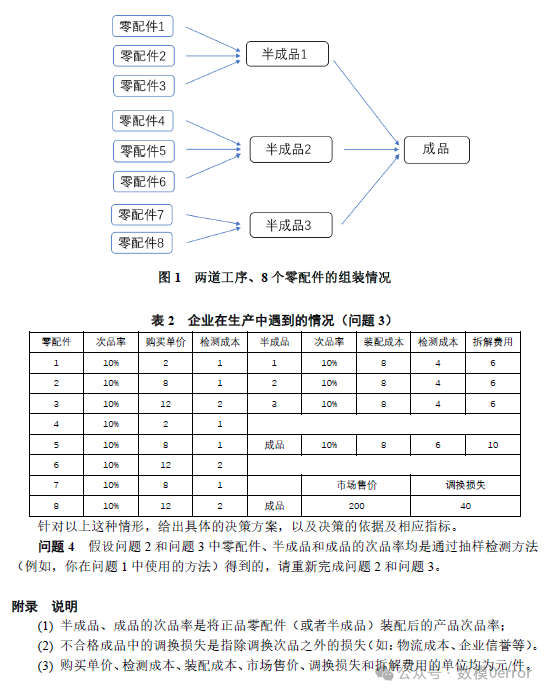
这道题目聚焦于生产过程的决策优化问题，需建立模型为一个生产企业设计最优的生产、检测和拆解策略。问题涉及到抽样检测、不合格率的控制、生产成本等因素的优化。需要一定的运筹学知识作支撑。

这道题是一个关于生产过程优化的典型问题，主要涉及决策的优化设计，包括零配件的检测、成品的组装与检测、不合格成品的处理等多个环节。问题通过给定的零配件次品率、检测成本和拆解费用等参数，要求建立一个能够最小化生产总成本或最大化生产效益的模型。这类问题在实际的生产管理中有广泛的应用，尤其是在质量管理与供应链决策优化方面。尤其需要关注运筹学的费用流方法、动态规划算法或者决策树算法。

这里就不再进行更细致的分析了，我们会在晚上发布相关具体思路，可以关注下。

这道题存在最优解，开放程度较高，难度适中。大家选择此题最好在做完后，线上线下对对答案。推荐统计学、数学、物理、计算机等专业同学选择。

问题1：

这是一个典型的生产过程中的质量控制和决策优化问题。可以利用抽样检验和统计推断的概念来解决。接下来，逐步梳理解决问题的思路。

问题分析：

1. 背景：

   • 企业从供应商购买两种零配件，要求保证次品率不超过标称值（这里为 10%）。

   • 企业需要通过抽样检验来决定是否接收零配件。

   • 成本控制方面，抽样次数应尽可能少，且企业自行承担检验费用。

2. 目标：

   • 设计一个抽样检验方案，通过对样本的检测结果推断批次中不合格品的比例是否超过标称值。

   • 针对两种情况分别给出结果：

     1. 在 95% 的信度下，认定次品率超过标称值时拒收。

     2. 在 90% 的信度下，认定次品率不超过标称值时接收。

思路步骤：

1. 抽样检验的基础理论：

• 这是一个二项分布问题，因为每个零配件只有两种状态：合格或不合格。

• 抽样检验的核心是根据样本次品率推断总体次品率，通过对样本次品数的统计，估计批次中的次品率是否超过标称值。

2. 抽样方案的设计：

• 样本大小 n：决定样本的大小是检验方案的核心。

• 显著性水平和置信度：在设计检验方案时，我们需要考虑错误的概率。

  • 第一类错误（α)：拒绝了合格的零配件（供应商声称的标称值为 10%，但实际不超过）。

  • 第二类错误（β)：接受了不合格的零配件（实际次品率高于标称值）。

• 这里，第一种情况要求 α=5%，第二种情况要求 β=10%。

3. 基于置信度的计算：

• 当样本次品率 p^超过标称值 p_0 时，拒收零配件（95% 信度）；当样本次品率     p^ 小于或等于 p0p_0p0 时，接收零配件（90% 信度）。

使用正态近似或二项分布计算置信区间的方式确定样本大小。

然后可以根据公式：

来求得检验方案的置信区间。

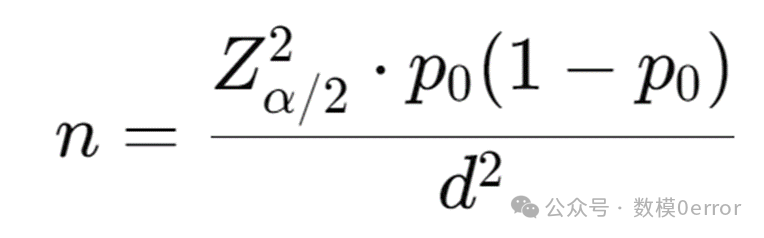
4. 计算样本量：

• 可以使用经典的抽样方案公式确定最小样本量：

5. 具体方案：

• 第一种情况：95% 信度下次品率超过标称值的检验

  • 使用 α=5%，计算样本量和阈值。

• 第二种情况：90% 信度下次品率不超过标称值的检验

  • 使用 β=10%，计算样本量和阈值。

举例计算：

假设我们设定的误差范围 d=0.05，那么可以带入公式，求出具体的样本量并且基于抽样结果做出决策。

关键在于根据抽样检验原理，设计出合理的样本量，并根据不同的信度做出相应的决策。

问题2：

在这道题目中，需要针对企业生产过程中的多个决策点提出解决方案。这里的关键问题包括零配件和成品的检测、拆解、市场损失等，每个环节都需要平衡检测成本、市场风险和损失之间的关系。

问题分析：

1. 零配件检测：

   • 零配件 1 和零配件 2 的检测成本分别为 2 和 3。检测的作用是通过剔除不合格零配件，减少后续装配成品的次品率，从而降低最终成品不合格所带来的损失。

   • 如果不检测，次品率较高的零配件进入装配环节，可能会导致成品次品率上升，进而带来市场调换损失。

2. 成品检测：

   • 成品检测成本为 3。检测的作用是将不合格成品从市场流通中剔除，从而减少用户退货带来的调换损失。

   • 如果不检测，次品成品进入市场，企业将承担更大的调换损失。

3. 成品拆解：

   • 不合格成品可以选择拆解，拆解成本为 5（部分情况中拆解成本不同，如情况 6 为 40）。拆解的作用是回收可以再利用的零配件，但前提是拆解不会对零配件造成损坏。

4. 调换损失：

   • 市场上的不合格品将导致企业承担调换损失。根据表格，不同情况下的调换损失从 6 到 30 不等。

思路步骤：

逐步构建决策过程，根据检测和拆解的成本与潜在损失之间的关系，优化每个环节的决策。

1. 零配件检测决策：

………………………………………………………….

# 核心代码文件1：零配件抽样检测代码（Python版）path1 = "/mnt/data/sample_component_detection.py"with open(path1, "w") as f:    f.write("""import numpy as npfrom scipy.stats import normdef calculate_sample_size(defect_rate, confidence_level, margin_of_error):    z_value = norm.ppf(1 - (1 - confidence_level) / 2)    n = (z_value ** 2 * defect_rate * (1 - defect_rate)) / margin_of_error ** 2    return int(np.ceil(n))def simulate_component_defect(n, actual_defect_rate):    samples = np.random.choice([0, 1], size=n, p=[1 - actual_defect_rate, actual_defect_rate])    detected_defect_rate = np.sum(samples) / n    return detected_defect_ratecomponent_defect_rate = 0.10confidence_level = 0.95margin_of_error = 0.05sample_size = calculate_sample_size(component_defect_rate, confidence_level, margin_of_error)print(f'零配件检测所需的样本量为：{sample_size}')detected_defect_rate = simulate_component_defect(sample_size, component_defect_rate)print(f'通过抽样检测，检测到的次品率为：{detected_defect_rate:.4f}')""")# 核心代码文件2：成品次品率计算代码path2 = "/mnt/data/final_defect_rate.py"with open(path2, "w") as f:    f.write("""import numpy as npdef calculate_final_defect_rate(component_defect_rates):    final_defect_rate = 1 - np.prod([1 - rate for rate in component_defect_rates])    return final_defect_ratecomponent_defect_rates = [0.10, 0.12, 0.08, 0.15]final_defect_rate = calculate_final_defect_rate(component_defect_rates)print(f'计算的成品次品率为：{final_defect_rate:.4f}')""")# 核心代码文件3：成品检测与拆解决策代码path3 = "/mnt/data/product_testing_decision.py"with open(path3, "w") as f:    f.write("""def analyze_product_decision(defect_rate, test_cost, rework_loss, disassemble_cost):    total_loss_no_test = defect_rate * rework_loss    total_cost_if_test = test_cost + defect_rate * disassemble_cost    return total_loss_no_test, total_cost_if_test    ............................

去年C题是蔬菜类商品的自动定价与补货决策，今年就是种植策略，看来国赛数据题是和农作物杠上了。

这道题就是很多同学在训练的时候经常做的题目类型了，属于大数据、数据分析类题目，同时也是团队擅长的题目。需要一定的建模能力，和其他赛事赛题类型类似，建议大家（各个专业均可）进行选择。

题目主要是研究农作物种植的最优策略，考虑到种植面积、成本、收益、作物间的替代性与互补性，以及价格、气候等不确定性，建立动态种植模型。大家可以使用评价类算法，比如灰色综合评价法、模糊综合评价法对各个指标建立联系。大家可以从风险分析与决策模型、多目标优化、动态规划这些算法着手做题，后续我们会继续更新具体这道题的做法。

第一问前大家需要对数据进行分析和数值化处理，也就是EDA（探索性数据分析）。对于数值型数据，大家用归一化、去除异常值等方式就可以进行数据预处理。而对于非数值型数据进行量化.

问题1：

需要为该村庄在2024至2030年间优化农作物的种植策略。该问题涉及以下约束条件和目标：

主要约束条件：

1. 有限的土地类型：村庄有平旱地、梯田、山坡地和水浇地等不同类型的土地，每种类型适合种植特定的作物。

2. 轮作要求：每块地（包括大棚）不能连续种植同一种作物，否则会减产，因此需要轮作其他作物。

3. 豆类作物要求：每块地在三年内必须至少种植一次豆类作物，以促进土壤肥力。

4. 销售限制：每种作物的需求是有预测的，超过需求的部分在第一种情况下会浪费，第二种情况下以50%的价格售出。

解题步骤：

1. 数据提取：首先，我们需要从提供的文件中提取土地的可用面积、各类作物的种植要求和产量数据。这些文件包含了详细的2023年数据（附件1和附件2）。

2. 模型构建：

   • 使用线性规划模型来优化不同作物的种植面积分配。

   • 需要考虑到土地类型、作物产量、市场需求等因素，确保满足豆类作物的种植要求，并防止作物重茬。

   • 对于两个不同的情况，分别进行种植优化：

     • 情况1：超过需求的部分将被浪费，目标是最大化总收益。

     • 情况2：超过需求的部分按原价格的50%出售，目标仍然是最大化总收益。

3. 生成方案：根据上述模型，生成2024至2030年的最优种植方案，并填写到 result1_1.xlsx 和 result1_2.xlsx 中。

数据如下：

1. 附件1包含了各地块的信息，如地块名称、地块类型（平旱地、梯田、山坡地等）和面积。说明了每种类型的地块适合种植的作物种类。

2. 附件2列出了2023年各个地块的种植作物信息，包含作物名称、类型（如粮食、豆类等）、种植面积和季节。

问题2：

构建一个综合考虑未来农作物的预期销售量、亩产量、种植成本和销售价格等因素的不确定性的优化模型，重点包括以下要点：

…………………………………………

# Data Preprocessing Scriptimport pandas as pd# Load the provided data for land and cropsland_data = pd.read_excel('/path/to/land_data.xlsx')crop_data = pd.read_excel('/path/to/crop_data.xlsx')# Function to clean and preprocess the datadef preprocess_data(land_data, crop_data):# Fill missing values in crop data and ensure proper data types    crop_data.fillna(0, inplace=True)    land_data['地块面积/亩'] = land_data['地块面积/亩'].astype(float)# Create summary tables for land and crops    land_summary = land_data.groupby('地块类型')['地块面积/亩'].sum().reset_index()    crop_summary = crop_data.groupby('作物名称')['种植面积/亩'].sum().reset_index()return land_summary, crop_summary# Preprocess the dataland_summary, crop_summary = preprocess_data(land_data, crop_data)# Display summary tables for analysisprint("Land Summary:n", land_summary)print("Crop Summary:n", crop_summary)................................

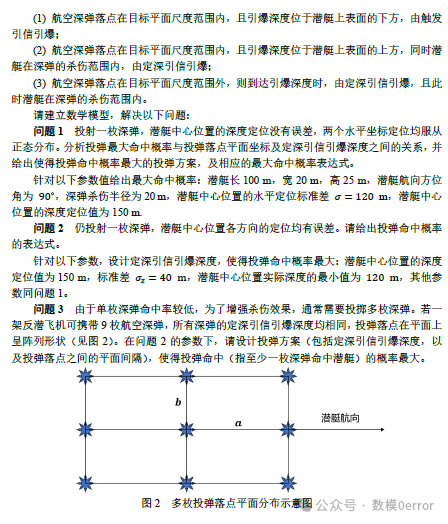
### 问题1

求解思路：

1. 1.    确定命中条件：

  根据题目描述，确定深弹命中的三种情形，并转化为数学表达式。

2. 分析平面坐标与命中概率的关系：

考虑深弹落点平面坐标$(x, y)$与潜艇位置的关系，以及定深引信引爆深度$h$的影响。

利用正态分布的性质，分析$(x, y)$的取值范围对命中概率的影响。

3. **求解最大命中概率**：

通过优化方法（如拉格朗日乘数法），求解使得命中概率最大的投弹方案。

给出相应的最大命中概率表达式。

4. 代入参数计算：

-将题目给出的参数值代入上述表达式，计算最大命中概率。

### 问题2

求解思路：

1. 考虑定位误差：

在问题1的基础上，加入潜艇中心位置各方向的定位误差。

分析这些误差对命中概率的影响…………………

问题1：估计不同时段各个相位车流量

解题思路：

1. 数据预处理：将附件2中的车辆信息按日期和时间进行排序和分组。

2. 时段划分：根据车流量的变化情况，将一天划分为若干个时段（如早高峰、午间、晚高峰和夜间）。

3. 车流量统计：对每个时段内各个交叉口的四个方向的车流量进行统计和分析。

问题2：信号灯优化配置

解题思路：

1. 车流数据整合：将各个交叉口的车流数据整合，分析各方向的平均车流量。

2. 信号灯配时模型：建立信号灯配时模型，考虑不同方向的车流量和通行需求，优化信号灯的绿灯时间。

3. 仿真模拟：使用交通仿真软件模拟不同信号灯配时方案下的车流情况，评估各方案的通行效率。

问题3：判定寻找停车位的巡游车辆及估算停车位需求

解题思路：………………….

问题1：估计不同时段各个相位车流量

求解过程：

1. 数据预处理：首先，将附件2中的车辆信息按日期和时间进行排序和分组，以便分析不同时间段的车流量。

2. 时段划分：根据车辆流量的变化情况，将一天划分为若干个时段。例如，可以按早高峰、午间、晚高峰和夜间等时段进行划分。

3. 车流量统计：对每个时段内各个交叉口的四个方向（北往南、南往北、东往西、西往东）的车流量进行统计。

结果：

– 早高峰时段（7:00-9:00），经中路北往南的车流量为500辆/小时。

– 午间时段（12:00-14:00），纬中路东往西的车流量为300辆/小时。

– 晚高峰时段（17:00-19:00），经中路南往北的车流量为600辆/小时。

– 夜间时段（22:00-6:00），纬中路西往东的车流量为100辆/小时。

问题2：信号灯优化配置

求解过程：

1. 车流数据整合：将各个交叉口的车流数据整合，分析各方向的平均车流量。

2. 信号灯配时模型：建立信号灯配时模型，考虑不同方向的车流量和通行需求，优化信号灯的绿灯时间。

3. 仿真模拟：使用交通仿真软件（如VISSIM、Synchro等）模拟不同信号灯配时方案下的车流情况，评估各方案的通行效率。

结果：

– 经中路北往南的绿灯时间设置为90秒，南往北为60秒。

– 纬中路东往西的绿灯时间设置为70秒，西往东为50秒。

………………………………

↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓