本次国赛预测题目难度,选题人数如下所示
难度评估 A:B:C= 1.8:1.3:1
D:E=1.5:1
选题人数 A:B:C= 1:1.5:2.8
D:E=0.5:1.2
C题一直以来都是竞赛难度最低、选题人数最多的一道本科生选题,近三年C题的选题人数一直都是总参赛队伍的一半左右,2023年六万支参赛队伍,C题选题队数2.8万。今年初步预计应该也是在3万左右。基于如此多的选题人数,本次我们将给大家带来两个版本的解题思路【思路、模型、代码完全不同】,下面进行第一版本的思路介绍
近年来,国赛在任何题目的数据预处理环节都设置了5-15分不等的数据预处理分值,因此数据预处理是必须进行的环节。数据预处理不仅仅是异常值、缺失值的处理,数据整合、数据可视化、描述性分析均是数据预处理工作。对于本次,我们可以进行异常值处理、数据整合、数据可视化、描述性分析进行数据的呈现。
数据预处理
- 异常值检测:题目中存在极端异常的数据,例如无论是亩产量还是种植成本存在极端数据,无论该数据是否真实我们都需要进行说明,以确保数据真实。
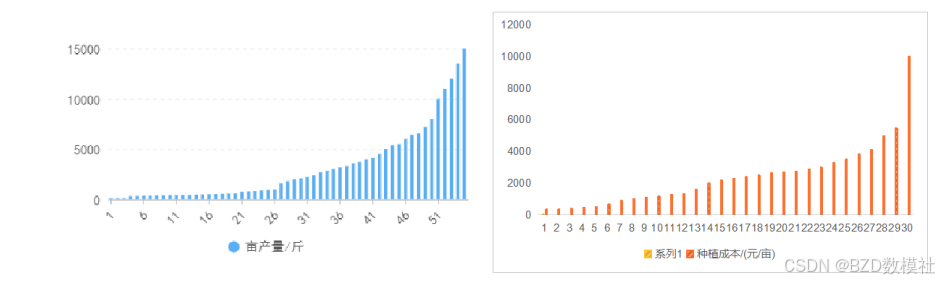
-
数据可视化、描述性分析:我们可以对题目给出的数据进行初步分析,以便后续建模,例如我们可以进行一些数据的可视化工作。
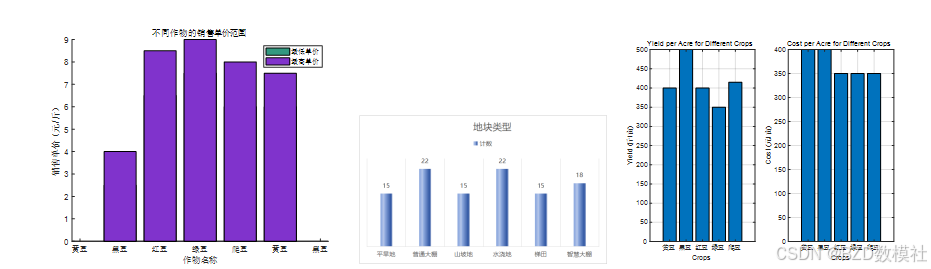

求解思路:
使用线性规划或整数规划,通过优化算法求解各地块每年应种植的作物组合,以达到收益最大化的目标。
针对问题1(1)和问题1(2)的不同假设,分别优化种植策略,并填入相应的模板文件。
创新点与改进点:
在模型中引入种植密度的约束,确保实际操作中的田间管理合理性,这在标准线性规划问题中较为少见。
不仅优化单一年的收益,而是优化未来7年的种植方案,确保作物轮作和收益的长远稳定。
问题二:考虑不确定性的最优种植方案
问题二在问题一的基础上,引入了未来销售量、种植成本和产量的波动,进一步增加了问题的复杂性。
1. 不确定性因素的引入
不确定性建模:
- 销售量变化:假设销售量在±5%波动,小麦和玉米的销售量以5%-10%的年增长率变化。
- 亩产量波动:每年由于气候等因素,作物产量会在±10%之间变化。
- 种植成本增长:假设种植成本每年增长5%。
- 价格变化:粮食类作物的价格基本稳定,而蔬菜价格每年增长5%左右,食用菌价格每年下降1%-5%。
模型调整:
- 建立一个随机规划模型或使用蒙特卡洛模拟,通过模拟销售量、产量、成本和价格的不确定性,进行多次情景分析,求得不确定条件下的最优种植方案。
具体来讲;
目标: 在引入不确定性因素(产量、价格、销售量和成本波动)的情况下,最大化期望收益。
期望收益最大化:
考虑作物
的销售量、产量和价格的不确定性,我们的目标是最大化期望收益:

问题三:农作物替代性和互补性分析
问题三要求在问题二的基础上,进一步考虑不同作物之间的替代性、互补性,以及销售量、价格和种植成本之间的相关性。
1. 引入作物之间的替代性和互补性
替代性和互补性分析:
- 可以通过协方差矩阵或者相关性系数来量化不同农作物之间的替代性和互补性。
- 替代性:例如某些豆类和谷物可能在市场上具有替代关系。
- 互补性:例如某些作物轮作可能会提升土壤肥力,使其互补性增强。
模型调整:
- 在问题二的基础上,加入农作物的替代性和互补性约束。通过引入相关系数矩阵调整种植方案,使整体组合效益更高。
目标函数:
- 目标依然是收益最大化,但需要在作物选择上综合考虑它们之间的替代性和互补性,从而优化整个系统的收益。
求解方法:
- 采用多目标优化模型,在最大化收益的同时,最小化作物之间的替代冲突,增强互补性。可以使用多目标优化算法如遗传算法或基于Pareto前沿的优化方法。
创新点与改进点:
- 利用作物间的相互作用来优化种植组合,增加实际种植策略的复杂度和现实性。
- 通过协方差矩阵的引入,使模型不仅是静态收益最大化,而是通过综合分析作物间的复杂关系,提高整体收益。
% MATLAB Code for Data Visualization
% Data for visualization (Example data from the table you provided)
crops = {‘黄豆’, ‘黑豆’, ‘红豆’, ‘绿豆’, ‘爬豆’}; % 作物名称
yield_per_acre = [400, 500, 400, 350, 415]; % 亩产量/斤
cost_per_acre = [400, 400, 350, 350, 350]; % 种植成本/(元/亩)
% For simplicity, we’ll average the min and max sales price for each crop
sales_price_min = [2.5, 6.5, 7.5, 6.0, 6.0]; % 销售单价下限/(元/斤)
sales_price_max = [4.0, 8.5, 9.0, 8.0, 7.5]; % 销售单价上限/(元/斤)
average_sales_price = (sales_price_min + sales_price_max) / 2; % 平均销售单价
% Bar plot for yield per acre and cost per acre
figure;
subplot(1, 2, 1);
bar(yield_per_acre);
set(gca, ‘xticklabel’, crops);
title(‘Yield per Acre for Different Crops’);
ylabel(‘Yield (斤/亩)’);
xlabel(‘Crops’);
grid on;
% Bar plot for cost per acre
subplot(1, 2, 2);
bar(cost_per_acre);
set(gca, ‘xticklabel’, crops);
title(‘Cost per Acre for Different Crops’);
ylabel(‘Cost (元/亩)’);
xlabel(‘Crops’);
grid on;
% Scatter plot for average sales price and yield per acre
figure;
scatter(average_sales_price, yield_per_acre, 100, ‘filled’);
title(‘Average Sales Price vs Yield per Acre’);
xlabel(‘Average Sales Price (元/斤)’);
ylabel(‘Yield per Acre (斤/亩)’);
grid on;
text(average_sales_price, yield_per_acre, crops, ‘VerticalAlignment’, ‘bottom’, ‘HorizontalAlignment’, ‘right’);
% 数据输入,作物名称,亩产量,种植成本和销售单价范围
crop_names = {‘黄豆’, ‘黑豆’, ‘红豆’, ‘绿豆’, ‘爬豆’}; % 作物名称
yield_per_acre = [400, 500, 400, 350, 415]; % 亩产量
cost_per_acre = [400, 400, 350, 350, 350]; % 种植成本
price_range_min = [2.5, 6.5, 7.5, 6.0, 6.0]; % 销售单价(最小值)
price_range_max = [4.0, 8.5, 9.0, 8.0, 7.5]; % 销售单价(最大值)
% 绘制亩产量柱状图
figure;
bar(yield_per_acre);
set(gca, ‘XTickLabel’, crop_names);
xlabel(‘作物名称’);
ylabel(‘亩产量(斤)’);
title(‘不同作物的亩产量’);
% 绘制种植成本柱状图
figure;
bar(cost_per_acre);
set(gca, ‘XTickLabel’, crop_names);
xlabel(‘作物名称’);
ylabel(‘种植成本(元/亩)’);
title(‘不同作物的种植成本’);
% 绘制销售单价范围柱状图
figure;
hold on;
bar(price_range_min, ‘FaceColor’, [0.2, 0.6, 0.5]);
bar(price_range_max, ‘FaceColor’, [0.5, 0.2, 0.8]);
set(gca, ‘XTickLabel’, crop_names);
xlabel(‘作物名称’);
ylabel(‘销售单价(元/斤)’);
title(‘不同作物的销售单价范围’);
legend({‘最低单价’, ‘最高单价’});
hold off;


评论(0)